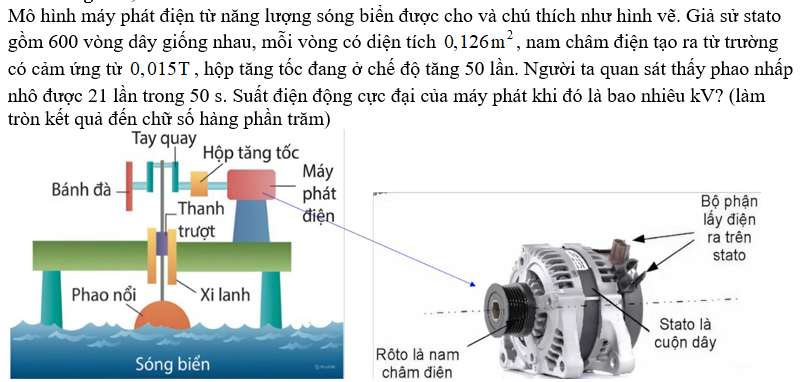
Một dây dẫn đang có dòng điện không đổi chạy qua. Trong khoảng thời gian \(t\), điện lượng chuyển qua tiết diện thẳng của dây dẫn là \(q\). Cường độ dòng điện I trong dây dẫn được tính bằng công thức nào sau đây?

a) Đúng

Tại vị trí thân tàu bị hỏng, áp suất nước biển là \(10,08 + 5 = 15,08\;{\rm{m}}\) nước biển \( \Rightarrow {\bf{b}}\) Đúng \({p_1}{V_1} = {p_2}{V_2} \Rightarrow 15,08 \cdot \frac{4}{3}\pi r_0^3 = 10,08 \cdot \frac{4}{3}\pi {r^3} \Rightarrow r \approx 1,15{r_0} \Rightarrow \) c) Sai

8 phút quan sát thì áp suất đã mất đi \(0,2{{\rm{p}}_0}\) và còn lại \(0,8{{\rm{p}}_0}\)

\( \Rightarrow 8\) phút sửa chữa thì áp suất mất đi \(1,5.0,2{{\rm{p}}_0} = 0,3{{\rm{p}}_0}\)

Người nhái có thể sửa chữa thân tàu trong thời gian tối đa là \(\frac{{0,8{{\rm{p}}_0} - 0,2{{\rm{p}}_0}}}{{3{{\rm{p}}_0}}} \cdot 8 = 16\) phút \( \Rightarrow \) d) Đúng

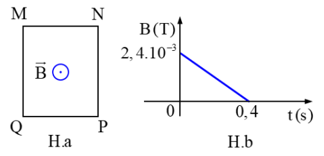
a) Sai. Theo quy tắc bàn tay phải \( \Rightarrow \) chiều dòng điện trên thanh từ M đến N

b) Sai. \(e = Blv = 0,5.0,5.4 = 1V\)

\(i = \frac{e}{R} = \frac{1}{{0,5}} = 2\;{\rm{A}}\)

c) Đúng. Theo định luật bảo toàn năng lượng

d) Đúng. \({F_t} = iBl = \frac{{eBl}}{R} = \frac{{{B^2}{l^2}v}}{R}\)

\( - {F_t} = ma \Rightarrow - \frac{{{B^2}{l^2}v}}{R} = m{v^\prime } \Rightarrow \frac{{{v^\prime }}}{v} = - \frac{{{B^2}{l^2}}}{{mR}} \Rightarrow {(\ln v)^\prime } = - \frac{{{B^2}{l^2}}}{{mR}} \Rightarrow \ln v = - \frac{{{B^2}{l^2}t}}{{mR}} + C\)

Khi \({\rm{t}} = 0\) thì \({\rm{v}} = {{\rm{v}}_0} \Rightarrow \ln {{\rm{v}}_0} = {\rm{C}} \Rightarrow \ln v = - \frac{{{B^2}{l^2}t}}{{mR}} + \ln {v_0} \Rightarrow v = {v_0}{e^{\frac{{ - {B^2}{l^2}t}}{{mR}}}}\)

Cách 2 (vi phân):

\( - {F_t} = ma \Rightarrow - \frac{{{B^2}{l^2}v}}{R} = ma \Rightarrow - \frac{{{B^2}{l^2}}}{R} \cdot \frac{{ds}}{{dt}} = m \cdot \frac{{dv}}{{dt}} \Rightarrow ds = - \frac{{mR}}{{{B^2}{l^2}}} \cdot dv\)

\( \Rightarrow \int_0^s d s = \int_4^0 {\left( { - \frac{{mR}}{{{B^2}{l^2}}}} \right)} \cdot dv \Rightarrow s = \int_4^0 {\left( { - \frac{{0,5 \cdot 5 \cdot {{10}^{ - 3}}}}{{0,{5^2} \cdot 0,{5^2}}}} \right)} \cdot dv = 0,16m = 16\;{\rm{cm}}\)

Cách 3:

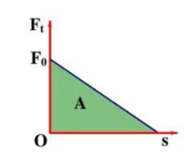
\({F_t} = iBl = \frac{{eBl}}{R} = \frac{{{B^2}{l^2}v}}{R} \Rightarrow {F_t}\) theo v là hàm bậc nhất (1)

Từ cách (2) có \(ds = - \frac{{mR}}{{{B^2}{l^2}}} \cdot dv \Rightarrow \;{\rm{s}}\) theo v là hàm bậc nhất (2)

Từ (1) và (2) \( \Rightarrow {{\rm{F}}_{\rm{t}}}\) theo s là hàm bậc nhất \( \Rightarrow |A| = \frac{1}{2}{F_0}s = \frac{1}{2} \cdot \frac{{{B^2}{l^2}{v_0}}}{R}s\)

Định lý động năng có \({W_{d0}} = |A| \Rightarrow \frac{1}{2}mv_0^2 = \frac{1}{2}\frac{{{B^2}{l^2}{v_0}}}{R} \cdot s \Rightarrow s = \frac{{m{v_0}R}}{{{B^2}{l^2}}} = \frac{{5 \cdot {{10}^{ - 3}} \cdot 4 \cdot 0,5}}{{0,{5^2} \cdot 0,{5^2}}} = 0,16m\)