Đáp án  ____

a) Đúng

Tại vị trí thân tàu bị hỏng, áp suất nước biển là \(10,08 + 5 = 15,08\;{\rm{m}}\) nước biển \( \Rightarrow {\bf{b}}\) Đúng \({p_1}{V_1} = {p_2}{V_2} \Rightarrow 15,08 \cdot \frac{4}{3}\pi r_0^3 = 10,08 \cdot \frac{4}{3}\pi {r^3} \Rightarrow r \approx 1,15{r_0} \Rightarrow \) c) Sai

8 phút quan sát thì áp suất đã mất đi \(0,2{{\rm{p}}_0}\) và còn lại \(0,8{{\rm{p}}_0}\)

\( \Rightarrow 8\) phút sửa chữa thì áp suất mất đi \(1,5.0,2{{\rm{p}}_0} = 0,3{{\rm{p}}_0}\)

Người nhái có thể sửa chữa thân tàu trong thời gian tối đa là \(\frac{{0,8{{\rm{p}}_0} - 0,2{{\rm{p}}_0}}}{{3{{\rm{p}}_0}}} \cdot 8 = 16\) phút \( \Rightarrow \) d) Đúng

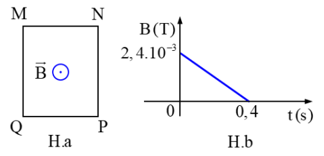
a) Sai. Theo quy tắc bàn tay phải \( \Rightarrow \) chiều dòng điện trên thanh từ M đến N

b) Sai. \(e = Blv = 0,5.0,5.4 = 1V\)

\(i = \frac{e}{R} = \frac{1}{{0,5}} = 2\;{\rm{A}}\)

c) Đúng. Theo định luật bảo toàn năng lượng

d) Đúng. \({F_t} = iBl = \frac{{eBl}}{R} = \frac{{{B^2}{l^2}v}}{R}\)

\( - {F_t} = ma \Rightarrow - \frac{{{B^2}{l^2}v}}{R} = m{v^\prime } \Rightarrow \frac{{{v^\prime }}}{v} = - \frac{{{B^2}{l^2}}}{{mR}} \Rightarrow {(\ln v)^\prime } = - \frac{{{B^2}{l^2}}}{{mR}} \Rightarrow \ln v = - \frac{{{B^2}{l^2}t}}{{mR}} + C\)

Khi \({\rm{t}} = 0\) thì \({\rm{v}} = {{\rm{v}}_0} \Rightarrow \ln {{\rm{v}}_0} = {\rm{C}} \Rightarrow \ln v = - \frac{{{B^2}{l^2}t}}{{mR}} + \ln {v_0} \Rightarrow v = {v_0}{e^{\frac{{ - {B^2}{l^2}t}}{{mR}}}}\)

Cách 2 (vi phân):

\( - {F_t} = ma \Rightarrow - \frac{{{B^2}{l^2}v}}{R} = ma \Rightarrow - \frac{{{B^2}{l^2}}}{R} \cdot \frac{{ds}}{{dt}} = m \cdot \frac{{dv}}{{dt}} \Rightarrow ds = - \frac{{mR}}{{{B^2}{l^2}}} \cdot dv\)

\( \Rightarrow \int_0^s d s = \int_4^0 {\left( { - \frac{{mR}}{{{B^2}{l^2}}}} \right)} \cdot dv \Rightarrow s = \int_4^0 {\left( { - \frac{{0,5 \cdot 5 \cdot {{10}^{ - 3}}}}{{0,{5^2} \cdot 0,{5^2}}}} \right)} \cdot dv = 0,16m = 16\;{\rm{cm}}\)

Cách 3:

\({F_t} = iBl = \frac{{eBl}}{R} = \frac{{{B^2}{l^2}v}}{R} \Rightarrow {F_t}\) theo v là hàm bậc nhất (1)

Từ cách (2) có \(ds = - \frac{{mR}}{{{B^2}{l^2}}} \cdot dv \Rightarrow \;{\rm{s}}\) theo v là hàm bậc nhất (2)

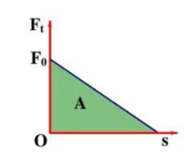
Từ (1) và (2) \( \Rightarrow {{\rm{F}}_{\rm{t}}}\) theo s là hàm bậc nhất \( \Rightarrow |A| = \frac{1}{2}{F_0}s = \frac{1}{2} \cdot \frac{{{B^2}{l^2}{v_0}}}{R}s\)

Định lý động năng có \({W_{d0}} = |A| \Rightarrow \frac{1}{2}mv_0^2 = \frac{1}{2}\frac{{{B^2}{l^2}{v_0}}}{R} \cdot s \Rightarrow s = \frac{{m{v_0}R}}{{{B^2}{l^2}}} = \frac{{5 \cdot {{10}^{ - 3}} \cdot 4 \cdot 0,5}}{{0,{5^2} \cdot 0,{5^2}}} = 0,16m\)