Cho tứ diện đều \(ABCD\) có cạnh bằng \(1\). Trên các mặt phẳng \(\left( {BCD} \right)\), \(\left( {CDA} \right)\), \(\left( {DAB} \right)\), \(\left( {ABC} \right)\) lần lượt lấy các điểm \({A_1}\), \({B_1}\), \({C_1}\), \({D_1}\) sao cho các đường thẳng \({A_1}{B_1}\), \({B_1}{C_1}\), \({C_1}{D_1}\), \({D_1}{A_1}\) lần lượt vuông góc với các mặt phẳng \(\left( {BCD} \right)\), \(\left( {CDA} \right)\), \(\left( {DAB} \right)\), \(\left( {ABC} \right)\). Biết thể tích khối tứ diện \({A_1}{B_1}{C_1}{D_1}\) bằng \(\frac{a}{b}\sqrt 2 \) với \(a\), \(b\) là các số nguyên dương và phân số \(\frac{a}{b}\) tối giản. Tính \(a + b\).
Quảng cáo
Trả lời:
Đáp án:
Đáp án: \(163\).
Gọi \(O\) là trọng tâm của tứ diện đều \(ABCD\).
Theo giả thiết, ta có \(OA \bot \left( {BCD} \right)\) nên \(OA{\rm{//}}\overrightarrow {{A_1}{B_1}} \)\( \Rightarrow \overrightarrow {{A_1}{B_1}} = {k_1}\overrightarrow {OA} \).
Tương tư: \(\overrightarrow {{B_1}{C_1}} = {k_2}\overrightarrow {OB} \), \(\overrightarrow {{C_1}{D_1}} = {k_3}\overrightarrow {OC} \) và \(\overrightarrow {{D_1}{A_1}} = {k_4}\overrightarrow {OD} \).
Ta có \(\overrightarrow {{A_1}{B_1}} + \overrightarrow {{B_1}{C_1}} + \overrightarrow {{C_1}{D_1}} + \overrightarrow {{D_1}{A_1}} = \overrightarrow 0 \)\[ \Leftrightarrow {k_1}\overrightarrow {OA} + {k_2}\overrightarrow {OB} + {k_3}\overrightarrow {OC} + {k_4}\overrightarrow {OD} = \overrightarrow 0 \].
Vì \(O\) là trọng tâm của tứ diện \(ABCD\) nên suy ra \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \)
Hay \({k_1}\overrightarrow {OA} + {k_1}\overrightarrow {OB} + {k_1}\overrightarrow {OC} + {k_1}\overrightarrow {OD} = \overrightarrow 0 \)
\( \Rightarrow \left( {{k_1} - {k_2}} \right)\overrightarrow {OB} + \left( {{k_1} - {k_3}} \right)\overrightarrow {OC} + \left( {{k_1} - {k_4}} \right)\overrightarrow {OD} = \overrightarrow 0 \). \(\left( * \right)\)
Do các vecto \(\overrightarrow {OB} \), \(\overrightarrow {OC} \) và \(\overrightarrow {OD} \) không đồng phẳng nên \(\left( * \right) \Leftrightarrow {k_1} = {k_2} = {k_3} = {k_4} = k\).
Chọn hệ trục tọa độ \(Oxyz\) sao cho \(A\left( {1;1;1} \right)\), \(B\left( {1; - 1; - 1} \right)\), \(C\left( { - 1;1; - 1} \right)\) và \(D\left( { - 1; - 1;1} \right)\).
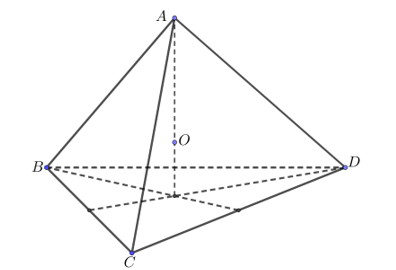
Khi đó: \[AB = BC = CD = DA = AC = BD = 2\sqrt 2 \].
Vì tứ diện \(ABCD\) có cạnh bằng \(1\) nên \(1\) đơn vị trên trên trục bằng \(2\sqrt 2 \)đơn vị độ dài.
Ta có :
\(\left( {BCD} \right)\) : \(x + y + z + 1 = 0\)
\(\left( {CDA} \right):x - y - z + 1 = 0\).
\(\left( {DAB} \right): - x + y - z + 1 = 0\).
\(\left( {ABC} \right): - x - y + z + 1 = 0\).
Gọi \({A_1}\left( {x;y;z} \right)\)
Vì \(\overrightarrow {{A_1}{B_1}} = k\overrightarrow {OA} \)\[ \Rightarrow {B_1}\left( {x + k;y + k;z + k} \right)\].
Tương tụ \({C_1}\left( {x + 2k;y;z} \right)\) và \({D_1}\left( {x + k;y + k;z - k} \right)\).
Ta có hệ \(\left\{ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{x + y + z + 1 = 0}\\{x + k - \left( {y + k} \right) - \left( {z + k} \right) + 1 = 0}\end{array}}\\{ - \left( {x + 2k} \right) + y - k + 1 = 0}\end{array}}\\{ - \left( {x + k} \right) - \left( {y + k} \right) + z - k + 1 = 0}\end{array}} \right.\)\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{x = - \frac{2}{3}}\\{y = - \frac{1}{3}}\end{array}}\\{\begin{array}{*{20}{c}}{z = 0}\\{k = \frac{2}{3}}\end{array}}\end{array}} \right.\).
Vậy \(\overrightarrow {{A_1}{B_1}} = \left( {\frac{2}{3};\frac{2}{3};\frac{2}{3}} \right)\), \(\overrightarrow {{B_1}{C_1}} = \left( {\frac{2}{3}; - \frac{2}{3}; - \frac{2}{3}} \right)\) và \(\overrightarrow {{C_1}{D_1}} = \left( { - \frac{2}{3};\frac{2}{3}; - \frac{2}{3}} \right)\).
Suy ra \(V = \frac{1}{6}\left| {\overrightarrow {{A_1}{B_1}} \cdot \left[ {\overrightarrow {{B_1}{C_1}} ,\overrightarrow {{C_1}{D_1}} } \right]} \right| = \frac{{16}}{{81}}\) (đơn vị thể tích trên trục)
Do đó \(V = \frac{{16}}{{81}} \cdot {\left( {\frac{1}{{2\sqrt 2 }}} \right)^3} = \frac{{\sqrt 2 }}{{162}}\) (đơn vị thể tích)
Vậy \(a + b = 163\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
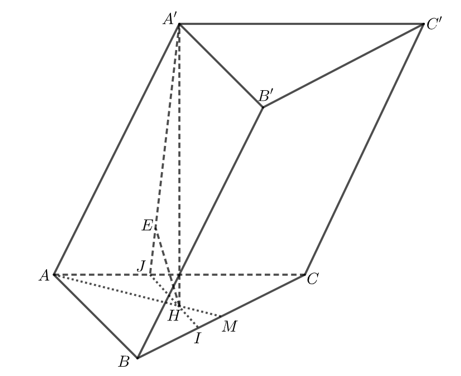
a) \(AB = AC = \frac{{BC}}{{\sqrt 2 }} = a\sqrt 2 \).
Gọi \(M\) là trung điểm của \(BC\). Ta có: \(AH = \frac{2}{3}AM = \frac{2}{3}.\frac{1}{2}BC = \frac{{2a}}{3}\).
Độ dài đường cao của lăng trụ là: \(A'H = \sqrt {A'{A^2} - A{H^2}} = \sqrt {{{\left( {2a} \right)}^2} - {{\left( {\frac{{2a}}{3}} \right)}^2}} = \frac{{4a\sqrt 2 }}{3}\).
Vậy khẳng định a đúng.
b) Thể tích khối lăng trụ đã cho là:
\({V_{ABC.A'B'C'}} = {S_{ABC}}.A'H = \frac{1}{2}AB.AC.A'H = \frac{1}{2}.a\sqrt 2 .a\sqrt 2 .\frac{{4a\sqrt 2 }}{3} = \frac{{4{a^3}\sqrt 2 }}{3}\).
Vậy khẳng định b sai.
c) Khoảng cách giữa hai đường thẳng \(BB'\) và \(AC\) là:
\(d\left( {BB';AC} \right) = d\left( {BB';\left( {ACC'A'} \right)} \right) = d\left( {B;\left( {ACC'A'} \right)} \right) = 3d\left( {H;\left( {ACC'A'} \right)} \right)\)
(Vì \(H\) là trọng tâm tam giác \(ABC\)).
Vậy khẳng định c đúng.
d) Kẻ \(HJ\) song song với \(AB\), \(J \in AC\), \(HJ \cap BC = I\)
\(HJ = \sqrt {A{H^2} - A{J^2}} = \sqrt {{{\left( {\frac{{2a}}{3}} \right)}^2} - {{\left( {\frac{1}{3}a\sqrt 2 } \right)}^2}} = \frac{{a\sqrt 2 }}{3}\)
Trong \(\left( {A'HJ} \right)\), kẻ \(HE \bot A'J\) tại \(E\)
Khi đó:
\(\frac{1}{{H{E^2}}} = \frac{1}{{A'{H^2}}} + \frac{1}{{H{J^2}}} = \frac{9}{{32{a^2}}} + \frac{9}{{2{a^2}}} = \frac{{9.17}}{{32{a^2}}} \Rightarrow HE = \frac{{4a\sqrt 2 }}{{3\sqrt {17} }}\).
\(d\left( {BB';AC} \right) = 3d\left( {H;\left( {ACC'A'} \right)} \right) = 3HE = \frac{{4a\sqrt {34} }}{{17}}\).
Vậy khẳng định d sai.
Lời giải
Đáp án: 5,4.
Gọi \(x,y\) (đơn vị: ha) lần lượt là diện tích đất trồng cây Cao su và cây Cà phê thì diện tích đất trồng cây Hồ tiêu là \(100 - x - y\). Điều kiện \[x,y \ge 0\].
Tổng diện tích trồng Cà phê và Hồ tiêu không được vượt quá diện tích trồng Cao su nên
\(y + \left( {100 - x - y} \right) \le x \Leftrightarrow x \ge 50\).
Diện tích trồng Hồ tiêu không được vượt quá 20 ha nên
\(100 - x - y \le 20 \Leftrightarrow x + y \ge 80\).
Diện tích trồng Cà phê không được vượt quá 3 lần diện tích trồng Hồ tiêu nên
\(y \le 3\left( {100 - x - y} \right) \Leftrightarrow 3x + 4y \le 300\).
Tổng lợi nhuận \(L\left( {x;y} \right) = 40x + 60y + 80\left( {100 - x - y} \right) = - 40x - 20y + 8000\) (triệu đồng).
Ta có hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 50\\x + y \ge 80\\3x + 4y \le 300\\x,y \ge 0\end{array} \right.\).
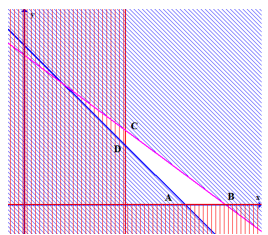
Miền nghiệm của bất phương trình là miền tứ giác \(ABCD\) với
\(A\left( {80;0} \right),B\left( {100;0} \right),C\left( {50;37,5} \right),D\left( {50;30} \right)\).
Vì \[L\left( A \right) = 4800,L\left( B \right) = 4000,L\left( C \right) = 5250,L\left( D \right) = 5400\] nên \(L\left( {x;y} \right)\)có giá trị lớn nhất là\(5400\) khi \(x = 50,y = 30\).
Vậy tổng lợi nhuận thu được hàng năm của trang trại đó lớn nhất là 5,4 tỷ đồng.Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
