Mặt cầu tâm \(I\) bán kính \(R > 0\) là tập hợp tất cả các điểm trong không gian cách \(I\) một khoảng bằng \(R\). Trong không gian với hệ tọa độ \(Oxyz\), đơn vị trên hệ trục là centimet, một tổ kiến có bề mặt là một mặt cầu tâm là gốc tọa độ và bán kính \(R = 6{\rm{cm}}\), ở điểm \(A\left( {20;0;0} \right)\) có \(10\) miếng mồi và ở điểm \(B\left( {0;20;0} \right)\) có \(3\) miếng mồi. Một con kiến trên bề mặt tổ, mỗi lần đi đến \(A\) hoặc \(B\) tha đúng một miếng mồi về tổ. Hỏi tổng quãng đường ngắn nhất con kiến đó đi là bao nhiêu centimet để con kiến tha hết \(13\) miếng mồi về tổ (kết quả làm tròn hàng đơn vị)?
Quảng cáo
Trả lời:
Đáp án:
Đáp án: 369.
Dễ thấy, \(A\left( {20;0;0} \right)\) và \(B\left( {0;20;0} \right)\) đều thuộc mặt phẳng \(\left( {Oxy} \right)\) nên đường đi ngắn nhất từ một điểm trên mặt cầu đến \(A\) (hoặc \(B\)) nằm trong mặt phẳng .
Đưa bài toán về hệ tọa độ \(Oxy\) với đường tròn tâm \(O\), bán kính \(6{\rm{cm}}\) và \(A\left( {20;0} \right)\); \(B\left( {0;20} \right)\).
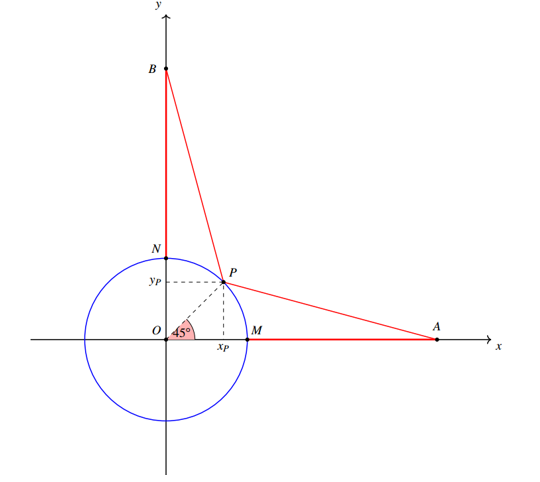
Để tổng quãng đường ngắn nhất, con kiến phải xuất phát và trở về mặt tổ tại điểm trên mặt cầu gần \(A\) và \(B\) nhất, lần lượt là các điểm \(M\left( {6;0} \right)\) và \(N\left( {0;6} \right)\).
Giả sử, con kiến sẽ lần lượt lấy các miếng mồi ở \(A\) rồi đến các miếng mồi ở \(B\). Tuy nhiên, khi lấy miếng mồi thứ \(10\) ở \(A\), con kiến sẽ về một điểm khác trên mặt tổ thay vì quay về \(M\) rồi đi theo đường cung tròn để đến \(N\).
Tổng quãng đường sẽ ngắn nhất khi con kiến mang miếng mồi thứ \(10\) về tổ tại điểm chính giữa cung tròn là \(P\), và từ đây đến \(B\) để lần lượt lấy \(3\) miếng mồi còn lại:
+ Tổng quãng đường để lấy \(10\) miếng mồi ở \(A\): \({T_1} = MA \times 9 \times 2 + MA + PA\).
+ Tổng quãng đường để lấy \(3\) miếng mồi ở \(B\): \({T_2} = PB + NB + NB \times 2 \times 2\).
Do đó: \({T_{\min }} = {T_1} + {T_2} = 19MA + 5NB + PA + PB\).
Ta có: \(\left\{ \begin{array}{l}{x_P} = 6 \times \cos 45^\circ = 3\sqrt 2 \\{y_P} = 6 \times \sin 45^\circ = 3\sqrt 2 \end{array} \right. \Rightarrow P\left( {3\sqrt 2 ;3\sqrt 2 } \right)\)
\( \Rightarrow PA = PB = \sqrt {{{\left( {20 - 3\sqrt 2 } \right)}^2} + {{\left( {3\sqrt 2 - 0} \right)}^2}} = 2\sqrt {109 - 30\sqrt 2 } \) và \(MA = NB = \sqrt {{{\left( {20 - 6} \right)}^2}} = 14\).
Vậy \({T_{\min }} = 19 \times 14 + 5 \times 14 + 2\sqrt {109 - 30\sqrt 2 } + 2\sqrt {109 - 30\sqrt 2 } \approx 369{\rm{cm}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
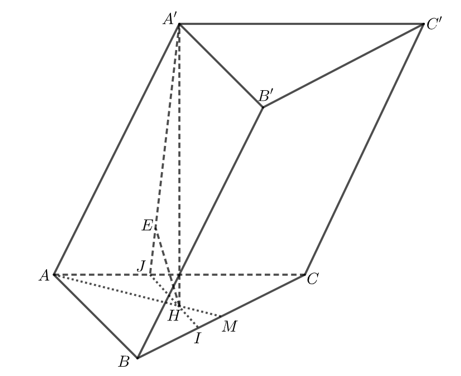
a) \(AB = AC = \frac{{BC}}{{\sqrt 2 }} = a\sqrt 2 \).
Gọi \(M\) là trung điểm của \(BC\). Ta có: \(AH = \frac{2}{3}AM = \frac{2}{3}.\frac{1}{2}BC = \frac{{2a}}{3}\).
Độ dài đường cao của lăng trụ là: \(A'H = \sqrt {A'{A^2} - A{H^2}} = \sqrt {{{\left( {2a} \right)}^2} - {{\left( {\frac{{2a}}{3}} \right)}^2}} = \frac{{4a\sqrt 2 }}{3}\).
Vậy khẳng định a đúng.
b) Thể tích khối lăng trụ đã cho là:
\({V_{ABC.A'B'C'}} = {S_{ABC}}.A'H = \frac{1}{2}AB.AC.A'H = \frac{1}{2}.a\sqrt 2 .a\sqrt 2 .\frac{{4a\sqrt 2 }}{3} = \frac{{4{a^3}\sqrt 2 }}{3}\).
Vậy khẳng định b sai.
c) Khoảng cách giữa hai đường thẳng \(BB'\) và \(AC\) là:
\(d\left( {BB';AC} \right) = d\left( {BB';\left( {ACC'A'} \right)} \right) = d\left( {B;\left( {ACC'A'} \right)} \right) = 3d\left( {H;\left( {ACC'A'} \right)} \right)\)
(Vì \(H\) là trọng tâm tam giác \(ABC\)).
Vậy khẳng định c đúng.
d) Kẻ \(HJ\) song song với \(AB\), \(J \in AC\), \(HJ \cap BC = I\)
\(HJ = \sqrt {A{H^2} - A{J^2}} = \sqrt {{{\left( {\frac{{2a}}{3}} \right)}^2} - {{\left( {\frac{1}{3}a\sqrt 2 } \right)}^2}} = \frac{{a\sqrt 2 }}{3}\)
Trong \(\left( {A'HJ} \right)\), kẻ \(HE \bot A'J\) tại \(E\)
Khi đó:
\(\frac{1}{{H{E^2}}} = \frac{1}{{A'{H^2}}} + \frac{1}{{H{J^2}}} = \frac{9}{{32{a^2}}} + \frac{9}{{2{a^2}}} = \frac{{9.17}}{{32{a^2}}} \Rightarrow HE = \frac{{4a\sqrt 2 }}{{3\sqrt {17} }}\).
\(d\left( {BB';AC} \right) = 3d\left( {H;\left( {ACC'A'} \right)} \right) = 3HE = \frac{{4a\sqrt {34} }}{{17}}\).
Vậy khẳng định d sai.
Lời giải
Đáp án: \(163\).
Gọi \(O\) là trọng tâm của tứ diện đều \(ABCD\).
Theo giả thiết, ta có \(OA \bot \left( {BCD} \right)\) nên \(OA{\rm{//}}\overrightarrow {{A_1}{B_1}} \)\( \Rightarrow \overrightarrow {{A_1}{B_1}} = {k_1}\overrightarrow {OA} \).
Tương tư: \(\overrightarrow {{B_1}{C_1}} = {k_2}\overrightarrow {OB} \), \(\overrightarrow {{C_1}{D_1}} = {k_3}\overrightarrow {OC} \) và \(\overrightarrow {{D_1}{A_1}} = {k_4}\overrightarrow {OD} \).
Ta có \(\overrightarrow {{A_1}{B_1}} + \overrightarrow {{B_1}{C_1}} + \overrightarrow {{C_1}{D_1}} + \overrightarrow {{D_1}{A_1}} = \overrightarrow 0 \)\[ \Leftrightarrow {k_1}\overrightarrow {OA} + {k_2}\overrightarrow {OB} + {k_3}\overrightarrow {OC} + {k_4}\overrightarrow {OD} = \overrightarrow 0 \].
Vì \(O\) là trọng tâm của tứ diện \(ABCD\) nên suy ra \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \)
Hay \({k_1}\overrightarrow {OA} + {k_1}\overrightarrow {OB} + {k_1}\overrightarrow {OC} + {k_1}\overrightarrow {OD} = \overrightarrow 0 \)
\( \Rightarrow \left( {{k_1} - {k_2}} \right)\overrightarrow {OB} + \left( {{k_1} - {k_3}} \right)\overrightarrow {OC} + \left( {{k_1} - {k_4}} \right)\overrightarrow {OD} = \overrightarrow 0 \). \(\left( * \right)\)
Do các vecto \(\overrightarrow {OB} \), \(\overrightarrow {OC} \) và \(\overrightarrow {OD} \) không đồng phẳng nên \(\left( * \right) \Leftrightarrow {k_1} = {k_2} = {k_3} = {k_4} = k\).
Chọn hệ trục tọa độ \(Oxyz\) sao cho \(A\left( {1;1;1} \right)\), \(B\left( {1; - 1; - 1} \right)\), \(C\left( { - 1;1; - 1} \right)\) và \(D\left( { - 1; - 1;1} \right)\).
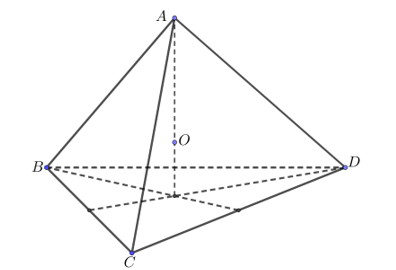
Khi đó: \[AB = BC = CD = DA = AC = BD = 2\sqrt 2 \].
Vì tứ diện \(ABCD\) có cạnh bằng \(1\) nên \(1\) đơn vị trên trên trục bằng \(2\sqrt 2 \)đơn vị độ dài.
Ta có :
\(\left( {BCD} \right)\) : \(x + y + z + 1 = 0\)
\(\left( {CDA} \right):x - y - z + 1 = 0\).
\(\left( {DAB} \right): - x + y - z + 1 = 0\).
\(\left( {ABC} \right): - x - y + z + 1 = 0\).
Gọi \({A_1}\left( {x;y;z} \right)\)
Vì \(\overrightarrow {{A_1}{B_1}} = k\overrightarrow {OA} \)\[ \Rightarrow {B_1}\left( {x + k;y + k;z + k} \right)\].
Tương tụ \({C_1}\left( {x + 2k;y;z} \right)\) và \({D_1}\left( {x + k;y + k;z - k} \right)\).
Ta có hệ \(\left\{ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{x + y + z + 1 = 0}\\{x + k - \left( {y + k} \right) - \left( {z + k} \right) + 1 = 0}\end{array}}\\{ - \left( {x + 2k} \right) + y - k + 1 = 0}\end{array}}\\{ - \left( {x + k} \right) - \left( {y + k} \right) + z - k + 1 = 0}\end{array}} \right.\)\( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{x = - \frac{2}{3}}\\{y = - \frac{1}{3}}\end{array}}\\{\begin{array}{*{20}{c}}{z = 0}\\{k = \frac{2}{3}}\end{array}}\end{array}} \right.\).
Vậy \(\overrightarrow {{A_1}{B_1}} = \left( {\frac{2}{3};\frac{2}{3};\frac{2}{3}} \right)\), \(\overrightarrow {{B_1}{C_1}} = \left( {\frac{2}{3}; - \frac{2}{3}; - \frac{2}{3}} \right)\) và \(\overrightarrow {{C_1}{D_1}} = \left( { - \frac{2}{3};\frac{2}{3}; - \frac{2}{3}} \right)\).
Suy ra \(V = \frac{1}{6}\left| {\overrightarrow {{A_1}{B_1}} \cdot \left[ {\overrightarrow {{B_1}{C_1}} ,\overrightarrow {{C_1}{D_1}} } \right]} \right| = \frac{{16}}{{81}}\) (đơn vị thể tích trên trục)
Do đó \(V = \frac{{16}}{{81}} \cdot {\left( {\frac{1}{{2\sqrt 2 }}} \right)^3} = \frac{{\sqrt 2 }}{{162}}\) (đơn vị thể tích)
Vậy \(a + b = 163\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
