Quanh một đa giác đều \(2n\) cạnh \(\left( {n \ge 6,n \in \mathbb{N}} \right)\) vẽ vòng tròn ngoại tiếp. Ba đỉnh bất kì của đa giác được gọi là cùng phía nếu tồn tại một nửa đường tròn chứa \(3\) đỉnh đó (các đầu mút của nửa đường tròn là các đỉnh của đa giác). Biết xác suất của biến cố “\(3\) đỉnh chọn bất kì cùng phía” bằng \(\frac{{33}}{{43}}.\) Tìm \(n?\)
Quảng cáo
Trả lời:
Đáp án:
Đáp án: \(22\).
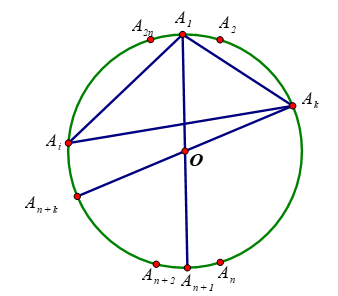
Đánh số các đỉnh là \({A_1},\,\,{A_2},\,\,{A_3},\,\,...,\,\,{A_{2n}}\).
* Số cách chọn 3 đỉnh bất kì: \(C_{2n}^3 = \frac{{\left( {2n} \right)!}}{{\left( {2n - 3} \right)!.3!}} = \frac{{2n.\left( {2n - 1} \right)\left( {2n - 2} \right)}}{6} = \frac{{2n\left( {2n - 1} \right)\left( {n - 1} \right)}}{3}\).
* Ba đỉnh cùng phía tạo thành một tam giác vuông hoặc tù.
+ Xét các tam giác vuông hoặc tù tại đỉnh \({A_1}\).
Đường chéo \({A_1}{A_{n + 1}}\) là đường kính của vòng tròn ngoại tiếp đa giác đều chia đường tròn ra làm hai phần, mỗi phần có \(n - 1\) điểm: từ \({A_2}\) đến \({A_n}\) và \({A_{n + 2}}\) đến \({A_{2n}}\).
Lấy đỉnh \({A_k},k = 2,3,...,n\), dựng đường kính \({A_k}{A_{n + k}}\).
Để tam giác \({A_1}{A_k}{A_i}\) vuông hoặc tù tại \({A_1}\) thì ta cần lấy đỉnh \({A_i}\) với \(i = n + k,n + k + 1,...,2n\)
Với \(k = 2\) thì \(i \in \left\{ {n + 2,n + 3,...,2n} \right\}\) Þ Có \(2n - \left( {n + 2} \right) + 1 = n - 1\) điểm
Với \(k = 3\) thì \(i \in \left\{ {n + 3,n + 4,...,2n} \right\}\) Þ Có \(2n - \left( {n + 3} \right) + 1 = n - 2\) điểm
…
Với \(k = n\) thì \(i \in \left\{ {2n} \right\}\) Þ Có 1 điểm
Þ Số tam giác vuông hoặc tù tại \({A_1}\) là \(\left( {n - 1} \right) + \left( {n - 2} \right) + ... + 2 + 1 = \frac{{n\left( {n - 1} \right)}}{2}\).
+ Tương tự với các tam giác vuông hoặc tù tại các đỉnh còn lại, ta có số tam giác vuông hoặc tù là
\(\frac{{n\left( {n - 1} \right)}}{2}.2n = {n^2}\left( {n - 1} \right)\)
Xác suất chọn được 3 đỉnh cùng phía là \(P = \frac{{{n^2}\left( {n - 1} \right)}}{{C_{2n}^3}} = \frac{{3{n^2}\left( {n - 1} \right)}}{{2n\left( {2n - 1} \right)\left( {n - 1} \right)}} = \frac{{3n}}{{2\left( {2n - 1} \right)}}\).
Do đó, ta có \(\frac{{3n}}{{2\left( {2n - 1} \right)}} = \frac{{33}}{{43}} \Leftrightarrow 43n = 22\left( {2n - 1} \right) \Leftrightarrow n = 22\).
Cách khác:
Trong một đa giác đều có \(2n\) đỉnh, bất kỳ một đường chéo nào đi qua tâm cũng chia đường tròn ngoại tiếp thành hai nửa đường tròn bằng nhau. Mỗi nửa đường tròn (tính cả hai đầu mút của đường kính) sẽ chứa đúng \(n + 1\) đỉnh.
+) Ta chọn một đỉnh bất kỳ trong số \(2n\) đỉnh làm đỉnh bắt đầu (gọi là đỉnh \({A_i}\)).
+) Từ \({A_i}\), ta kẻ một đường kính sang đỉnh đối diện. Nửa đường tròn tính theo chiều kim đồng hồ bắt đầu từ \({A_i}\) sẽ bao gồm \({A_i}\) và \(n\) đỉnh tiếp theo.
+) Để bộ 3 đỉnh "cùng phía" và nhận \({A_i}\) làm đỉnh đầu tiên, ta chỉ cần chọn thêm 2 đỉnh nữa từ \(n\) đỉnh còn lại trong nửa đường tròn đó. Số cách chọn 2 đỉnh từ \(n\) đỉnh là: \(C_n^2\).
+) Có tất cả \(2n\) đỉnh có thể đóng vai trò là "đỉnh bắt đầu" \({A_i}\). Với mỗi đỉnh bắt đầu đó, có \(C_n^2\) cách chọn 2 đỉnh còn lại để tạo thành một nhóm 3 đỉnh nằm gọn trong nửa đường tròn khởi đầu từ \({A_i}\).
Xác suất chọn được 3 đỉnh cùng phía là \(P = \frac{{2n.C_n^2}}{{C_{2n}^3}} = \frac{{3n}}{{2\left( {2n - 1} \right)}}\).
Do đó, ta có \(\frac{{3n}}{{2\left( {2n - 1} \right)}} = \frac{{33}}{{43}} \Leftrightarrow 43n = 22\left( {2n - 1} \right) \Leftrightarrow n = 22\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 0,05.
Gọi \(\Omega \) là không gian mẫu của phép thử.
Ta có \(n\left( \Omega \right) = 9 \cdot 8 \cdot 7 \cdot 6\).
Gọi \(A\) là biến cố lấy được \(4\) quả cầu ghi các số có tổng bằng \(15\). Ta giả sử các số đó \(a\), \(b\),\(c\), \(d\).
Theo giả thiết \(a + b + c + d = 15\).
Suy ra \(\left( {a,b,c,d} \right) \in \left\{ {\left( {1;2;3;9} \right),\left( {1,2,4,8} \right),\left( {1,2,5,7} \right),\left( {1,3,5,6} \right),\left( {1,3,4,7} \right),\left( {2,3,4,6} \right)} \right\}\)
\( \Rightarrow n\left( A \right) = 6 \times 4!\).
Vậy xác suất cẩn tính \(P\left( A \right) = \frac{{6 \times 4!}}{{9 \times 8 \times 7 \times 6}} \approx 0,05\).
Câu 2
Lời giải
Chọn B
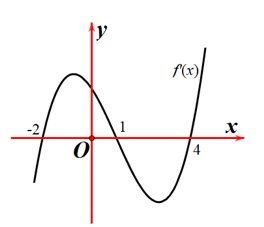
Hàm số đạt cực đại khi \(y = f'\left( x \right)\) đổi dấu từ dương sang âm. Quan sát đồ thị của đạo hàm \(y = f'\left( x \right)\) thì hàm số sẽ đạt cực đại tại \(x = 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.