Bốn ngư dân góp vốn mua chung một chiếc thuyền. Số tiền người đầu đóng góp bằng nửa tổng số tiền của ba người còn lại. Số tiền người thứ hai đóng góp bằng \(\frac{1}{3}\) tổng số tiền của ba người còn lại. Số tiền người thứ ba đóng góp bằng \(\frac{1}{4}\) tổng số tiền 3 người còn lại. Biết người thứ tư đóng góp 260 triệu đồng. Chiếc thuyền này được mua bao nhiêu tỉ đồng?
Quảng cáo
Trả lời:
Đáp án:
Đáp án: \(1,2\).
Gọi số tiền người thứ nhất, thứ hai, thứ ba đóng góp lần lượt là \(x,\,\,y,\,\,z\) \(\left( {x,\,\,y,\,\,z > 0} \right)\) (triệu đồng).
Số tiền người đầu đóng góp bằng nửa tổng số tiền của ba người còn lại nên:
\(x = \frac{1}{2}\left( {y + z + 260} \right) \Leftrightarrow 2x - y - z = 260\).
Số tiền người thứ hai đóng góp bằng \(\frac{1}{3}\) tổng số tiền của ba người còn lại nên:
\(y = \frac{1}{3}\left( {x + z + 260} \right) \Leftrightarrow - x + 3y - z = 260\).
Số tiền người thứ ba đóng góp bằng \(\frac{1}{4}\) tổng số tiền 3 người còn lại nên:
\(z = \frac{1}{4}\left( {x + y + 260} \right) \Leftrightarrow - x - y + 4z = 260\).
Khi đó ta có hệ phương trình: \(\left\{ \begin{array}{l}2x - y - z = 260\\ - x + 3y - z = 260\\ - x - y + 4z = 260\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 400\\y = 300\\z = 240\end{array} \right.\).
Giá của chiếc thuyền là: \(400 + 300 + 240 + 260 = 1200\) (triệu đồng) hay \(1,2\) tỉ đồng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 0,05.
Gọi \(\Omega \) là không gian mẫu của phép thử.
Ta có \(n\left( \Omega \right) = 9 \cdot 8 \cdot 7 \cdot 6\).
Gọi \(A\) là biến cố lấy được \(4\) quả cầu ghi các số có tổng bằng \(15\). Ta giả sử các số đó \(a\), \(b\),\(c\), \(d\).
Theo giả thiết \(a + b + c + d = 15\).
Suy ra \(\left( {a,b,c,d} \right) \in \left\{ {\left( {1;2;3;9} \right),\left( {1,2,4,8} \right),\left( {1,2,5,7} \right),\left( {1,3,5,6} \right),\left( {1,3,4,7} \right),\left( {2,3,4,6} \right)} \right\}\)
\( \Rightarrow n\left( A \right) = 6 \times 4!\).
Vậy xác suất cẩn tính \(P\left( A \right) = \frac{{6 \times 4!}}{{9 \times 8 \times 7 \times 6}} \approx 0,05\).
Lời giải
Đáp án: 8,64.
Ta có: \(\overrightarrow {DA} = \left( { - 3;0;0} \right)\), \(\overrightarrow {DB} = \left( {0; - 4;0} \right)\) và \(\overrightarrow {DC} = \left( {0;0; - 5} \right)\).
Dễ thấy: \[\left\{ \begin{array}{l}\overrightarrow {DA} .\overrightarrow {DB} = 0 \Rightarrow DA \bot DB\\\overrightarrow {DB} .\overrightarrow {DC} = 0 \Rightarrow DB \bot DC\\\overrightarrow {DC} .\overrightarrow {DA} = 0 \Rightarrow DC \bot DA\end{array} \right.\] nên các điểm \(A\left( {0;4;5} \right)\), \(B\left( {3;0;5} \right)\), \(C\left( {3;4;0} \right)\), \(D\left( {3;4;5} \right)\) là các đỉnh của một hình hộp chữ nhật với \(DA = 3\), \(DB = 4\) và \(DC = 5\).
Gọi \(S = d\left( {A,MD} \right) + d\left( {B,MD} \right) + d\left( {C,MD} \right)\).
Ta có \(d\left( {C,MD} \right) = DC = 5\) nên \(S\) lớn nhất khi \(d\left( {A,MD} \right) + d\left( {B,MD} \right)\) lớn nhất.
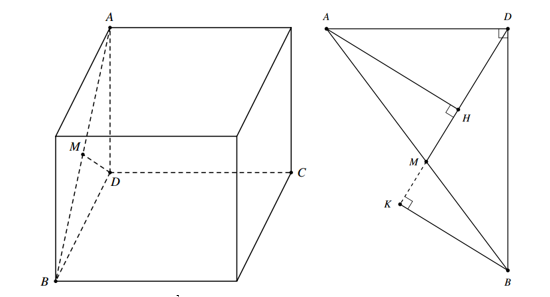
Xét \(\Delta DAB\) trong mặt phẳng \(\left( {DAB} \right)\): \(d\left( {A,MD} \right) + d\left( {B,MD} \right) \le AM + BM = AB\).
Dấu bằng xảy ra khi \(M\) là hình chiếu của \(D\) lên \(AB\).
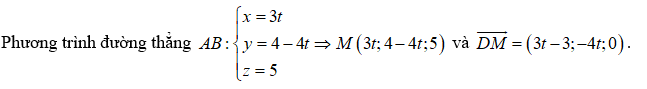
Do \[DM \bot AB \Rightarrow \overrightarrow {DM} .\overrightarrow {AB} = 0 \Rightarrow \left( {3t - 3} \right) \times 3 - 4t \times \left( { - 4} \right) = 0 \Leftrightarrow t = \frac{9}{{25}} \Rightarrow M\left( {\frac{{27}}{{25}};\frac{{64}}{{25}};5} \right)\].
Vậy \[a + b + c = \frac{{27}}{{25}} + \frac{{64}}{{25}} + 5 = 8,64\].
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.