Cho hàm số \(y = f\left( x \right) = {x^2}.{e^x}\).
Quảng cáo
Trả lời:
Ta có \(f'\left( x \right) = {\left( {{x^2}.{e^x}} \right)^\prime } = 2x.{e^x} + {x^2}.{e^x} = \left( {{x^2} + 2x} \right).{e^x}\). d). Đúng
\(f'\left( x \right) = 0 \Leftrightarrow \left( {{x^2} + 2x} \right).{e^x} = 0 \Leftrightarrow {x^2} + 2x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 2\end{array} \right.\). a). Sai
\(f\left( { - 1} \right) = \frac{1}{e};\,f\left( 0 \right) = 0;\,f\left( 1 \right) = e \Rightarrow 0 < \frac{1}{e} < e\). \(\mathop {\min }\limits_{\left[ { - 1;\,1} \right]} f\left( x \right) = 0\). b). Sai
BBT
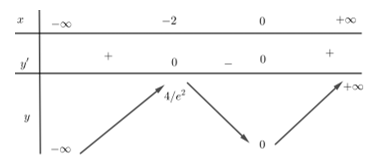
Hàm số đồng biến trên \(\left( { - \infty ;\, - 2} \right)\) và \(\left( {0;\, + \infty } \right)\); nghịch biến trên \(\left( { - 2;\,0} \right)\). c). Sai
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: \(11,7\)
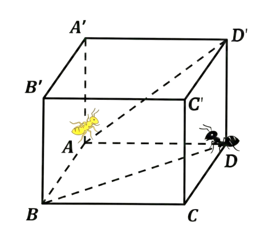
Chọn hệ trục tọa độ như hình vẽ
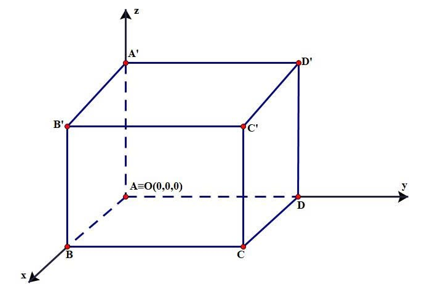
Lúc khó: \(A\left( {0,0,0} \right),B\left( {20,0,0} \right),D\left( {0,20,0} \right),D\prime \left( {0,20,20} \right)\)
- Vectơ chỉ phương của đường thẳng \(AD\prime \) là \(\overrightarrow {AD'} = \left( {0,20,20} \right)\) và độ dài \(\left| {\overrightarrow {AD'} } \right| = 20\sqrt 2 \)
Kiến vàng đi thẳng từ \(A\) đến \(D'\) với vận tốc \(2{\rm{ cm/s}}\)
⇒ Vectơ vận tốc kiến vàng: \({\vec v_1} = \frac{{\overrightarrow {AD'} }}{{\left| {\overrightarrow {AD'} } \right|}}.{v_1} = \left( {0;\sqrt 2 ;\sqrt 2 } \right)\)
- Vectơ chỉ phương đường thẳng \(DB\) là \(\overrightarrow {DB} = \left( {20, - 20,0} \right)\) và độ dài \(\left| {\overrightarrow {DB} } \right| = 20\sqrt 2 \)
Kiến đen đi thẳng từ \(D\) đến \(B\) với vận tốc \(3{\rm{ cm/s}}\).
⇒ Vectơ vận tốc kiến đen: \({\vec v_2} = \frac{{\overrightarrow {BD} }}{{\left| {BD} \right|}}.{v_2} = \left( {\frac{3}{{\sqrt 2 }}, - \frac{3}{{\sqrt 2 }},0} \right)\)
Gọi \(t\) (giây) là thời gian kể từ lúc xuất phát.
* Vị trí kiến vàng tại thời điểm t là \(M\left( t \right) = \left( {0,\sqrt 2 t,\sqrt 2 t} \right)\)
* Vị trí kiến đen tại thời điểm t là \(N\left( t \right) = \left( {\frac{3}{{\sqrt 2 }}t,20 - \frac{3}{{\sqrt 2 }}t,0} \right)\)
Khoảng cách giữa hai chú kiến là \(MN\) và
\(M{N^2}(t){\rm{ }} = {\left( {\frac{3}{{\sqrt 2 }}t} \right)^2} + {\left( {20 - \frac{3}{{\sqrt 2 }}t - \sqrt 2 t} \right)^2} + {(\sqrt 2 t)^2} = 19{t^2} - 100\sqrt 2 t + 400\)
Giá trị nhỏ nhất của \(M{N^2}\) đạt được khi: \(t = \frac{{50\sqrt 2 }}{{19}}\)
Khi đó: \(M{N_{\min }} = \sqrt {\frac{{2600}}{{19}}} \approx 11,7\left( {\;{\rm{cm}}} \right)\)
Lời giải
Đáp án: –37.
+ Gọi C: “lấy được 3 bi đỏ từ hộp\[C\]”
\[{B_i}\]: “lấy \[i\]bi đỏ hộp\[B\]”
\({A_i}\): “Lấy \[i\]bi đổ hộp\[A\]”
+ Ta có
\[\begin{array}{l}P\left( C \right) = P\left( {{A_0}} \right)P\left( {{B_1}/{A_0}} \right)P\left( {C/{B_1}} \right) + P\left( {{A_0}} \right)P\left( {{B_2}/{A_0}} \right)P\left( {C/{B_2}} \right) + P\left( {{A_1}} \right)P\left( {{B_1}/{A_1}} \right)P\left( {C/{B_1}} \right) + \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + P\left( {{A_1}} \right)P\left( {{B_2}/{A_1}} \right)P\left( {C/{B_2}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\, = \frac{3}{8}.\frac{{2.3}}{{C_5^2}}.\frac{1}{{C_6^3}} + \frac{3}{8}.\frac{1}{{C_5^2}}.\frac{{C_4^3}}{{C_6^3}} + \frac{5}{8}.\frac{{2.3}}{{C_5^2}}.\frac{1}{{C_6^3}} + \frac{5}{8}.\frac{{C_3^2}}{{C_5^2}}.\frac{{C_4^3}}{{C_6^3}} = \frac{3}{{40}} \Rightarrow a = 3;b = 40.\end{array}\]
Vậy \[a - 40 = - 37\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.