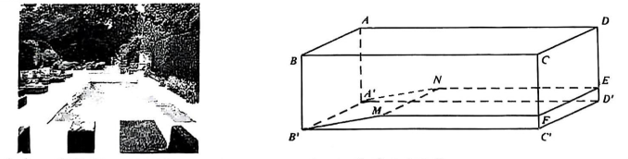
Một chiếc má bay thương mại đang bay trên bầu trời theo một đường thẳng từ \[D\] đến \(E\), có hình chiếu trên mặt đất là đoạn \(CB\). Tại vị trí \(D\) thì máy bay cách mặt đất \(9000\,m\), tại vị trí \(E\) thì máy bay cách mặt đất \(12000\,m\). Một ra đa được đặt trên mặt đất tại vị trí \(O\) cách \(C\) khoảng \(20000\,m\), cách \(B\) khoảng \(16000\,m\) và \(\widehat {BOC} = {90^o}\), phạm vi theo dõi của ra đa là \(20\,km\). Xét hệ trục tọa độ \(Oxyz\) (đơn vị trên mỗi trục là \(1000\,m\)) với \(O\) là vị trí đặt ra đa, \(B\) thuộc tia \(Oy\), \(C\) thuộc tia \(Ox\).
![Một chiếc má bay thương mại đang bay trên bầu trời theo một đường thẳng từ \[D\] đến \(E\), (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/02/blobid9-1770785501.png)
Một chiếc má bay thương mại đang bay trên bầu trời theo một đường thẳng từ \[D\] đến \(E\), có hình chiếu trên mặt đất là đoạn \(CB\). Tại vị trí \(D\) thì máy bay cách mặt đất \(9000\,m\), tại vị trí \(E\) thì máy bay cách mặt đất \(12000\,m\). Một ra đa được đặt trên mặt đất tại vị trí \(O\) cách \(C\) khoảng \(20000\,m\), cách \(B\) khoảng \(16000\,m\) và \(\widehat {BOC} = {90^o}\), phạm vi theo dõi của ra đa là \(20\,km\). Xét hệ trục tọa độ \(Oxyz\) (đơn vị trên mỗi trục là \(1000\,m\)) với \(O\) là vị trí đặt ra đa, \(B\) thuộc tia \(Oy\), \(C\) thuộc tia \(Ox\).
![Một chiếc má bay thương mại đang bay trên bầu trời theo một đường thẳng từ \[D\] đến \(E\), (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/02/blobid9-1770785501.png)
Quảng cáo
Trả lời:
a) Sai
Ta có vị trí của ra đa là \(O(0;0;0);\,D(20;0;9)\)
Vậy \(OD = \sqrt {{{20000}^2} + {{9000}^2}} \approx 22000\)(\(m\))
b) Đúng
Vị trí cuối cùng của máy bay là \(E(0;16;12)\)
Gọi điểm chính giữa của \(DE\) là điểm \(I \Rightarrow I\left( {10;8;\frac{{21}}{2}} \right)\)
Vậy cao độ của điểm \(I\) là khoảng cách của máy bay so với mặt đất, nên khi này máy bay cách mặt đất \(\frac{{21}}{2} \times 1000 = 10500\,m\).
c) Đúng
Ta có \(\overrightarrow {DE} ( - 20;16;3)\)
Phương trình đường thẳng \(DE:\,\left\{ \begin{array}{l}x = 20 - 20t\\y = 16t\\z = 9 + 3t\end{array} \right.,\,t \in \mathbb{R}\)
Với \(t = \frac{1}{5} \Rightarrow P\left( {16;\frac{{16}}{5};\frac{{48}}{5}} \right) \in DE\)
Vậy trên quãng đường bay từ \(D\) đến \(E\), máy bay sẽ bay qua vị trí \(P\left( {16;\frac{{16}}{5};\frac{{48}}{5}} \right)\).
d) Đúng
Gọi \(M \in DE \Rightarrow M\left( {20 - 20t;16t;9 + 3t} \right)\)
\(OM \le 20 \Rightarrow {\left( {20 - 20t} \right)^2} + {(16t)^2} + {(9 + 3t)^2} \le 400\)
\( \Leftrightarrow 665{t^2} - 746t + 81 \le 0 \Leftrightarrow \frac{{81}}{{665}} \le t \le 1\)
Với \(t = \frac{{81}}{{665}} \Rightarrow {M_1}\left( {\frac{{2336}}{{133}};\frac{{1296}}{{665}};\frac{{6228}}{{665}}} \right) \in DE\)
Với \(t = 1 \Rightarrow {M_2}\left( {0;16;12} \right) \in DE\)
\( \Rightarrow {M_1}{M_2} \approx 22600\,m\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: \(11,7\)
Chọn hệ trục tọa độ như hình vẽ
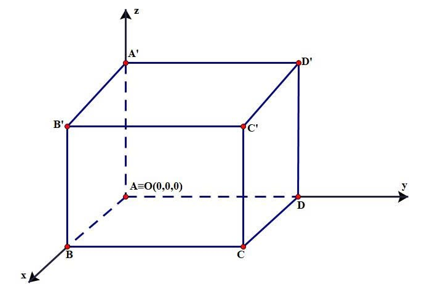
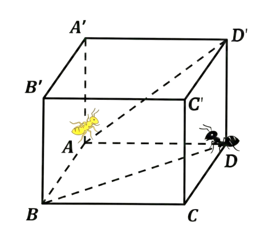
Lúc khó: \(A\left( {0,0,0} \right),B\left( {20,0,0} \right),D\left( {0,20,0} \right),D\prime \left( {0,20,20} \right)\)
- Vectơ chỉ phương của đường thẳng \(AD\prime \) là \(\overrightarrow {AD'} = \left( {0,20,20} \right)\) và độ dài \(\left| {\overrightarrow {AD'} } \right| = 20\sqrt 2 \)
Kiến vàng đi thẳng từ \(A\) đến \(D'\) với vận tốc \(2{\rm{ cm/s}}\)
⇒ Vectơ vận tốc kiến vàng: \({\vec v_1} = \frac{{\overrightarrow {AD'} }}{{\left| {\overrightarrow {AD'} } \right|}}.{v_1} = \left( {0;\sqrt 2 ;\sqrt 2 } \right)\)
- Vectơ chỉ phương đường thẳng \(DB\) là \(\overrightarrow {DB} = \left( {20, - 20,0} \right)\) và độ dài \(\left| {\overrightarrow {DB} } \right| = 20\sqrt 2 \)
Kiến đen đi thẳng từ \(D\) đến \(B\) với vận tốc \(3{\rm{ cm/s}}\).
⇒ Vectơ vận tốc kiến đen: \({\vec v_2} = \frac{{\overrightarrow {BD} }}{{\left| {BD} \right|}}.{v_2} = \left( {\frac{3}{{\sqrt 2 }}, - \frac{3}{{\sqrt 2 }},0} \right)\)
Gọi \(t\) (giây) là thời gian kể từ lúc xuất phát.
* Vị trí kiến vàng tại thời điểm t là \(M\left( t \right) = \left( {0,\sqrt 2 t,\sqrt 2 t} \right)\)
* Vị trí kiến đen tại thời điểm t là \(N\left( t \right) = \left( {\frac{3}{{\sqrt 2 }}t,20 - \frac{3}{{\sqrt 2 }}t,0} \right)\)
Khoảng cách giữa hai chú kiến là \(MN\) và
\(M{N^2}(t){\rm{ }} = {\left( {\frac{3}{{\sqrt 2 }}t} \right)^2} + {\left( {20 - \frac{3}{{\sqrt 2 }}t - \sqrt 2 t} \right)^2} + {(\sqrt 2 t)^2} = 19{t^2} - 100\sqrt 2 t + 400\)
Giá trị nhỏ nhất của \(M{N^2}\) đạt được khi: \(t = \frac{{50\sqrt 2 }}{{19}}\)
Khi đó: \(M{N_{\min }} = \sqrt {\frac{{2600}}{{19}}} \approx 11,7\left( {\;{\rm{cm}}} \right)\)
Lời giải
Đáp án: –37.
+ Gọi C: “lấy được 3 bi đỏ từ hộp\[C\]”
\[{B_i}\]: “lấy \[i\]bi đỏ hộp\[B\]”
\({A_i}\): “Lấy \[i\]bi đổ hộp\[A\]”
+ Ta có
\[\begin{array}{l}P\left( C \right) = P\left( {{A_0}} \right)P\left( {{B_1}/{A_0}} \right)P\left( {C/{B_1}} \right) + P\left( {{A_0}} \right)P\left( {{B_2}/{A_0}} \right)P\left( {C/{B_2}} \right) + P\left( {{A_1}} \right)P\left( {{B_1}/{A_1}} \right)P\left( {C/{B_1}} \right) + \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + P\left( {{A_1}} \right)P\left( {{B_2}/{A_1}} \right)P\left( {C/{B_2}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\, = \frac{3}{8}.\frac{{2.3}}{{C_5^2}}.\frac{1}{{C_6^3}} + \frac{3}{8}.\frac{1}{{C_5^2}}.\frac{{C_4^3}}{{C_6^3}} + \frac{5}{8}.\frac{{2.3}}{{C_5^2}}.\frac{1}{{C_6^3}} + \frac{5}{8}.\frac{{C_3^2}}{{C_5^2}}.\frac{{C_4^3}}{{C_6^3}} = \frac{3}{{40}} \Rightarrow a = 3;b = 40.\end{array}\]
Vậy \[a - 40 = - 37\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.