Trong các đa thức dưới đây, đa thức nào có hệ số tự do?
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: C
Hệ số tự do là hệ số không chứa biến.
Vậy trong các đa thức đã cho chỉ có đa thức \(4{x^3} + {x^2} - x - 5\) có hệ số tự do là \( - 5\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số người đi trồng cây của mỗi đội A; B; C lần lượt là: \(x;y;z\) (người), (\(x;y;z \in {\mathbb{N}^*}\))
Vì có tất cả \(130\) người đi trồng cây nên \(x + y + z = 130\)
Vì số cây mỗi đội trồng được là bằng nhau và số cây mỗi người đội A; B; C trồng được theo thứ tự là \(2;3;4\) nên số cây mỗi người trồng được sẽ tỉ lệ nghịch với số người trong đội.
Ta có: \(x.2 = y.3 = z.4\)\( \Rightarrow \frac{{2x}}{{12}} = \frac{{3y}}{{12}} = \frac{{4z}}{{12}}\) hay \(\frac{x}{6} = \frac{y}{4} = \frac{z}{3}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\frac{x}{6} = \frac{y}{4} = \frac{z}{3} = \frac{{x + y + z}}{{6 + 4 + 3}} = \frac{{130}}{{13}} = 10\)
Khi đó, \(\frac{x}{6} = 10\) nên \(x = 10.6 = 60\)
\(\frac{y}{4} = 10\) nên \(y = 10.4 = 40\)
\(\frac{z}{3} = 10\) nên \(z = 10.3 = 30\)
Số người đi trồng cây của ba đội A: B; C lần lượt là \(60;40;30\) người.
Lời giải
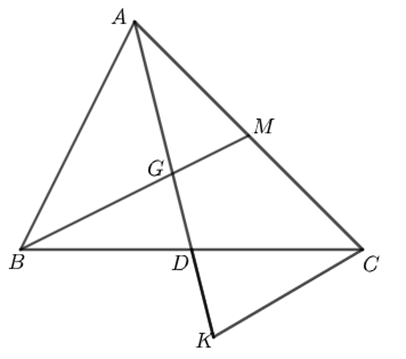
a) Xét tam giác \(MBC\) có:
\(MB < MC + CB\) (bất đẳng thức tam giác)
Cộng 2 vế với \(MA\) ta được:
\(MB + MA < MC + MA + CB\)
Mà \(MC + MA = CA\) nên \(MB + MA < CA + CB\)
b) Vì \(BM\)song song với \(CK\)nên \(\widehat {GBD} = \widehat {KCD}\) (hai góc so le trong)
Xét tam giác \(GDB\) và tam giác \(KDC\) ta có:
\(\widehat {GBD} = \widehat {KCD}\) (chứng minh trên)
\(\widehat {GDB} = \widehat {KDC}\) (hai góc đối đỉnh)
\(BD = DC\) (Do \(AD\) là đường trung tuyến nên \(D\) là trung điểm \(BC\)).
Do đó, \(\Delta GDB = \Delta KDC\) (g.c.g)
Suy ra, \(GD = DA\) (hai cạnh tương ứng)
Mà \(DK = \frac{1}{3}AD\) nên \(GD = \frac{1}{3}AD\).
Mà \(AD\) là trung tuyến nên \(G\) là trọng tâm tam giác \(ABC\).
Suy ra, \(BM\) là đường trung tuyến của \(\Delta ABC\) nên \(M\) là trung điểm của \(AC\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.