Căn bậc hai số học của \(\frac{9}{{25}}\) là
Quảng cáo
Trả lời:
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
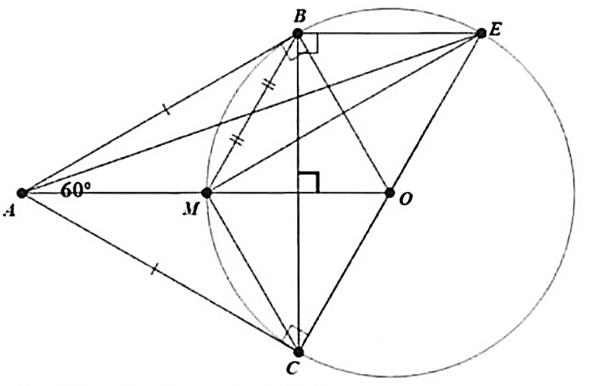
a) Theo tính chất hai tiếp tuyến cắt nhau, ta có \(AB = AC\) nên tam giác \(ABC\) cân tại \(A.\)
Hơn nữa, ta có \(\widehat {BAC} = 60^\circ \) nên tam giác \(ABC\) là tam giác đều.
Vì \(AB,\,\,AC\) là các tiếp tuyến nên \(AB \bot OB\,;\,\,AC \bot OC.\)
Xét tứ giác \(ABOC\) có \[\widehat {BAC} + \widehat {ABO} + \widehat {ACO} + \widehat {BOC} = 360^\circ \].
Suy ra \[\widehat {BOC} = 360^\circ - \widehat {BAC} - \widehat {ABO} - \widehat {ACO} = 360^\circ - 90^\circ - 90^\circ - 60^\circ = 120^\circ .\]
Do đó (nhỏ) \[ = \widehat {BOC} = 120^\circ \] suy ra (lớn) \[ = 360^\circ - \] (nhỏ)\[ = 240^\circ .\]
Vậy tam giác \(ABC\) đều; \[\widehat {BOC} = 120^\circ \,;\] (lớn) \[ = 240^\circ .\]
b) Tam giác \(ABC\) cân, theo tính chất hai tiếp tuyến cắt nhau thì \(AO\) là phân giác \(\widehat {BAC}\)
nên \(AO\) là đường cao, tức là
Ta có \(OB = OC = OE = \frac{1}{2}CE,\) theo tính chất trung tuyến tam giác vuông thì tam giác \(BCE\) vuông tại \(B\) tức là
Từ (1) và (2) suy ra \(BE\,{\rm{//}}\,AO.\)
Dễ thấy \(\widehat {BOM} = 60^\circ \) và \(OB = OM\) nên \(\Delta OBM\) đều, suy ra
Hơn nữa, dễ thấy \(\widehat {BOE} = 180^\circ - \widehat {BOC} = 60^\circ \) và \(OB = OE\) nên \(\Delta OBE\) đều hay
Từ (3) và (4) suy ra \(MB = BE = EO = OM\) nên tứ giác \(MBEO\) là hình thoi, suy ra \(ME \bot OB.\)
Mặt khác, \(OB \bot AB\) nên \(ME\,{\rm{//}}\,AB.\) Kết hợp \(BE\,{\rm{//}}\,MA\) (vì \(BE\,{\rm{//}}\,AO\,).\)
Do đó \(ABEM\) là hình bình hành nên \(AE\) đi qua trung điểm của đoạn thẳng \(BM.\)
Vậy \(BE\,{\rm{//}}\,AO\) và \(AE\) đi qua trung điểm của đoạn thẳng \(BM.\)
Lời giải
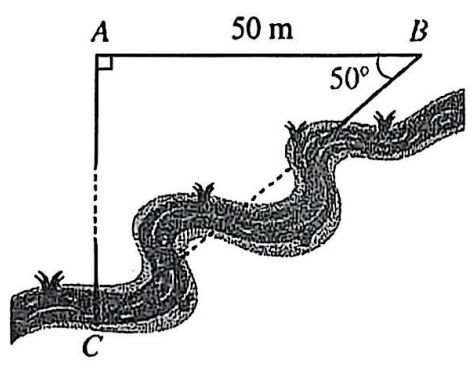
a) Xét tam giác vuông \(ABC\), theo tỉ số lượng giác, ta có: \({\rm{cos}}\,B = \frac{{AB}}{{BC}}\).
Suy ra \(BC = \frac{{AB}}{{{\rm{cos}}\,B}} = \frac{{50}}{{{\rm{cos}}\,50^\circ }} \approx 77,8\,\,{\rm{(m}}).\)
Vậy \(BC \approx 77,8\,\,{\rm{m}}.\)
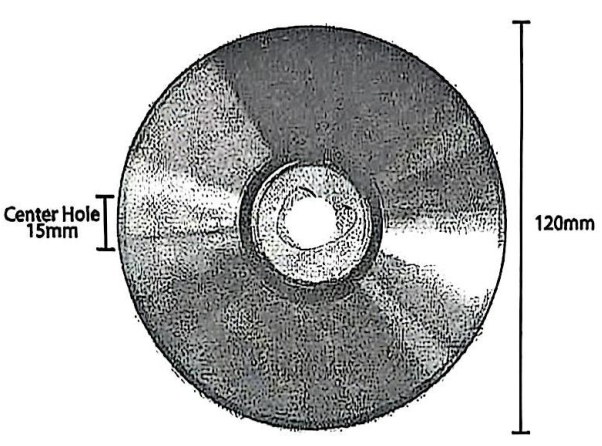
b) Bán kính ngoài của đĩa CD là: \(R = \frac{{120}}{2} = 60{\rm{\;(mm)}} = 6{\rm{\;(cm)}}{\rm{.}}\)
Bán kính lỗ tròn rỗng bên trong là \(r = \frac{{15}}{2} = 7,5{\rm{\;(mm)}} = 0,75{\rm{\;(cm)}}{\rm{.}}\)
Diện tích bề mặt đĩa (hình vành khăn) là:
\(S = \pi \left( {{R^2} - {r^2}} \right) = 3,14 \cdot \left( {{6^2} - 0,{{75}^2}} \right) \approx 111,27{\rm{\;}}\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
Vậy diện tích bề mặt của đĩa CD khoảng \(111,27{\rm{\;c}}{{\rm{m}}^2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(37,7\,\,{{\rm{m}}^2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.