(1,0 điểm).
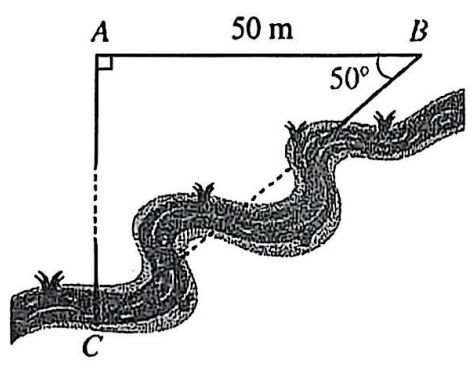
a) Hình vẽ bên dưới mô tả ba vị trí \(A,B,C\) là ba đỉnh của một tam giác vuông có vị trí xung quanh một khúc sông. Biết \(AB = 50{\rm{\;m}}\,,\,\,\widehat {ABC} = 50^\circ .\) Tính khoảng cách \(BC\) theo đơn vị mét (làm tròn kết quả đến hàng phần chục).

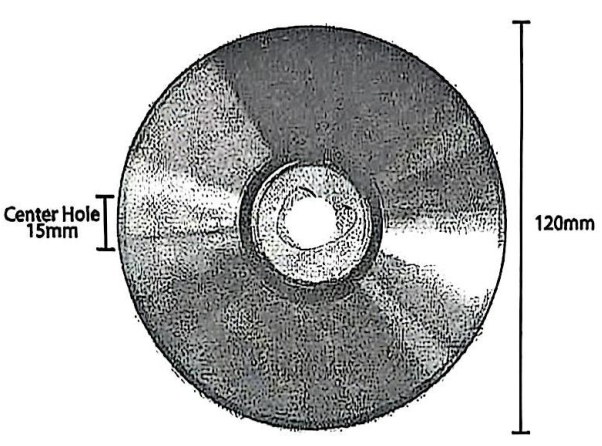
b) Một chiếc đĩa CD có dạng hình vành khăn giới hạn mép ngoài của đĩa và lỗ rỗng ở tâm đĩa. Biết đường kính ngoài của đĩa là \(120\,\,{\rm{mm}}\) và đường kính lỗ tròn rỗng ở tâm đĩa là \(15\,\,{\rm{mm}}\,{\rm{.}}\) Cho \(\pi \approx 3,14,\) hãy tính diện tích bề mặt của đĩa CD đó theo đơn vị \({\rm{c}}{{\rm{m}}^2}\) và chính xác đến hàng phần trăm.

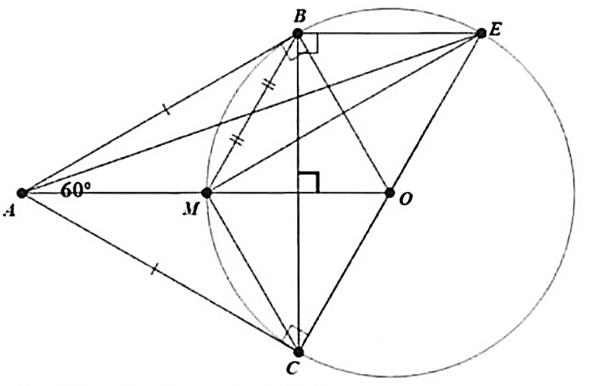
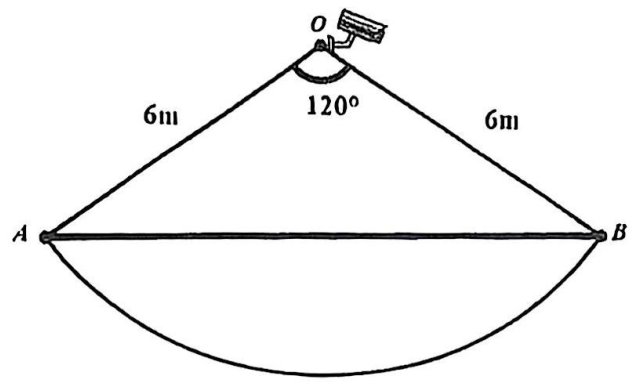
a) Theo tính chất hai tiếp tuyến cắt nhau, ta có \(AB = AC\) nên tam giác \(ABC\) cân tại \(A.\)

Hơn nữa, ta có \(\widehat {BAC} = 60^\circ \) nên tam giác \(ABC\) là tam giác đều.

Vì \(AB,\,\,AC\) là các tiếp tuyến nên \(AB \bot OB\,;\,\,AC \bot OC.\)

Xét tứ giác \(ABOC\) có \[\widehat {BAC} + \widehat {ABO} + \widehat {ACO} + \widehat {BOC} = 360^\circ \].

Suy ra \[\widehat {BOC} = 360^\circ - \widehat {BAC} - \widehat {ABO} - \widehat {ACO} = 360^\circ - 90^\circ - 90^\circ - 60^\circ = 120^\circ .\]

Do đó $\text{sđ\hspace{0.17em}\hspace{0.17em}}\stackrel{⏜}{BC}$ (nhỏ) \[ = \widehat {BOC} = 120^\circ \] suy ra $\text{sđ\hspace{0.17em}\hspace{0.17em}}\stackrel{⏜}{BC}$ (lớn) \[ = 360^\circ - \] (nhỏ)\[ = 240^\circ .\]

Vậy tam giác \(ABC\) đều; \[\widehat {BOC} = 120^\circ \,;\] $\text{sđ\hspace{0.17em}\hspace{0.17em}}\stackrel{⏜}{BC}$ (lớn) \[ = 240^\circ .\]

b) Tam giác \(ABC\) cân, theo tính chất hai tiếp tuyến cắt nhau thì \(AO\) là phân giác \(\widehat {BAC}\)

 nên \(AO\) là đường cao, tức là $AO\perp BC.\left(1\right)$

Ta có \(OB = OC = OE = \frac{1}{2}CE,\) theo tính chất trung tuyến tam giác vuông thì tam giác \(BCE\) vuông tại \(B\) tức là $BE\perp BC.\left(2\right)$

Từ (1) và (2) suy ra \(BE\,{\rm{//}}\,AO.\)

Dễ thấy \(\widehat {BOM} = 60^\circ \) và \(OB = OM\) nên \(\Delta OBM\) đều, suy ra $MO=MO=BO.\left(3\right)$

Hơn nữa, dễ thấy \(\widehat {BOE} = 180^\circ - \widehat {BOC} = 60^\circ \) và \(OB = OE\) nên \(\Delta OBE\) đều hay $OE=OB=BE.\left(4\right)$

Từ (3) và (4) suy ra \(MB = BE = EO = OM\) nên tứ giác \(MBEO\) là hình thoi, suy ra \(ME \bot OB.\)

Mặt khác, \(OB \bot AB\) nên \(ME\,{\rm{//}}\,AB.\) Kết hợp \(BE\,{\rm{//}}\,MA\) (vì \(BE\,{\rm{//}}\,AO\,).\)

Do đó \(ABEM\) là hình bình hành nên \(AE\) đi qua trung điểm của đoạn thẳng \(BM.\)

Vậy \(BE\,{\rm{//}}\,AO\) và \(AE\) đi qua trung điểm của đoạn thẳng \(BM.\)

a) Từ phương trình thứ nhất, ta có \(y = 4x - 7\).

Thay \(y = 4x - 7\) vào phương trình thứ hai ta được: \(x + 3\left( {4x - 7} \right) = 5\).

Suy ra \(x + 12x - 21 = 5\) nên \(13x = 26\) hay \(x = 2\).

Thay \(x = 2\) vào \(y = 4x - 7\), ta được: \(y = 4.2 - 7 = 1\).

Vậy hệ phương trình có nghiệm duy nhất là \(\left( {2\,;\,\,1} \right).\)

b) \(\left( { - x + 6} \right)\left( {2x - 4} \right) = 0\)

\( - x + 6 = 0\) hoặc \(2x - 4 = 0\)

\(x = 6\) hoặc \(x = 2\).

Vậy phương trình có hai nghiệm \(x = 6;x = 2\)

c) \(4 - 7\left( {x - 3} \right) \le 2\left( {x - 1} \right)\)

\(4 - 7x + 21 \le 2x - 2\)

\( - 9x \le - 27\)

\(x \ge 3\)

Vậy nghiệm của bất phương trình là \(x \ge 3\).