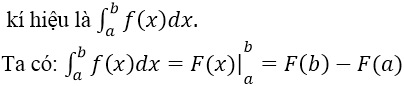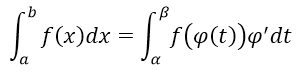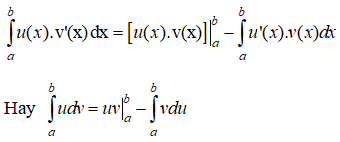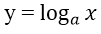Nêu định nghĩa và các phương pháp tính tích phân.

Xem lời giải

Câu hỏi trong đề: Giải tích 12 - Phần giải tích !!

Quảng cáo

Trả lời:

Giải bởi Vietjack

• Định nghĩa

Cho hàm số y = f(x) liên tục trên [a; b] , F(x) là một nguyên hàm của f(x) trên [a; b]. Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x)

Giải bài tập Giải tích 12 | Để học tốt Toán 12

• Phương pháp tính tích phân

a) Đổi biến số:

Định lí 1: Cho hàm số f(x) liên tục trên [a; b]. Giả sử hàm số x = φ(t) có đạo hàm liên tục trên đoạn [ α;β] sao cho φ(α) = a; φ(β) = βvà a ≤ φ(t) ≤ b với mọi t ∈ [α;β]. Khi đó:

Giải bài tập Giải tích 12 | Để học tốt Toán 12

b) Tích phân từng phần

Nếu u = u(x) và v = v(x) là hai hàm số có đạo hàm liên tục trên đoạn [a; b] thì:

Giải bài tập Giải tích 12 | Để học tốt Toán 12

Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tìm giá trị lớn nhất và nhỏ nhất của hàm số: f(x)=2sinx+sin2x trên nửa khoảng $[0; \frac{3}{2} π]$

Xem đáp án

Lời giải

Giải bài 8 trang 147 sgk Giải tích 12 | Để học tốt Toán 12

Câu 2

Nêu tính chất của hàm số mũ, hàm số logarit, mối liên hệ giữa đồ thị của hàm số mũ cà hàm số logarit cùng cơ số.

Xem đáp án

Lời giải

1. Hàm số mũ

Cho số a > 0 và a ≠ 1. Hàm số y = $a^{x}$ được gọi là hàm số mũ cơ số a.

Các tính chất của hàm số mũ y = $a^{x}$

Tập xác định	(-∞; +∞)
Đạo hàm	y’= $a^{x}$ .lna
Chiều biến thiên	+ Nếu a > 1 thì hàm số luôn đồng biến + Nếu 0 < a < 1 thì hàm số nghịch biến
Tiệm cận	Trục Ox là tiệm cận ngang
Đồ thị	Đi qua các điểm (0; 1); (1; a) Nằm phía trên trục hoành ( y = $a^{x}$ > 0 mọi x)

2. Hàm Logarit

Cho số a > 0 và a ≠ 1 . Hàm số y = logax được gọi là hàm số logarit cơ số a

Giải bài tập Giải tích 12 | Để học tốt Toán 12

Tập xác định	(0; +∞)
Đạo hàm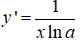
Chiều biến thiên	+ Nếu a > 1: hàm số luôn đồng biến + Nếu 0 < a < 1: hàm số luôn nghịch biến
Tiệm cận	Trục Oy là tiệm cận đứng
Đồ thị	Đi qua các điểm (1; 0); (a; 1) Nằm bên phải trục tung.

3. Liên hệ giữa đồ thị của hàm số mũ và hàm số logarit cùng cơ số: Đồ thị của hàm số mũ và đồ thị của hàm số logarit đối xứng nhau qua đường phân giác góc phần tư thứ nhất.

Câu 3