Phòng luyện đề thi giữa kì 1 năm học 2026-2027 tất cả các môn lớp 1-12

✕

Giảm 50% Kích hoạt VIP

Kích hoạt VIP

Tạo VIP

Câu hỏi:

13/07/2024 14,599

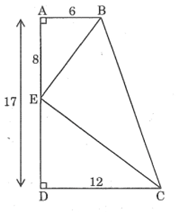
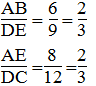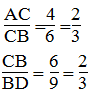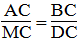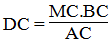Cho hình thang vuông ABCD ( $∠$ A = $∠$ D = $90^{0}$ ) AB = 6cm, CD = 12cm, AD = 17cm. Trên cạnh AD, đặt đoạn AE = 8cm. Chứng minh $∠$ (BEC) = $90^{0}$

Xem lời giải

Câu hỏi trong đề: Giải Sách Bài Tập Toán 8 Tập 2 !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Ta có: AD = AE + DE

Suy ra: DE = AD – AE = 17 – 8 = 9cm

Xét $△$ ABE và $△$ DEC, ta có:

$∠$ A = $∠$ D = $90^{0}$ (1)

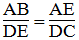
Mà : Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Suy ra: Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8 (2)

Từ (1) và (2) suy ra : $△$ ABE đồng dạng $△$ DEC (c.g.c)

Suy ra: $∠$ ABE = $∠$ DEC

Trong $△$ ABE ta có: $∠$ A = $90^{0}$ ⇒ $∠$ (AEB) + $∠$ (ABE) = $90^{0}$

Suy ra: $∠$ (AEB) + $∠$ (DEC) = $90^{0}$

Lại có: $∠$ (AEB) + $∠$ (BEC) + $∠$ (DEC) = $180^{0}$ (kề bù)

Vậy : $∠$ (BEC) = $180^{0}$ - ( $∠$ (AEB) + $∠$ (DEC)) = $180^{0}$ - $90^{0}$ = $90^{0}$

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác ABC vuông tại A, AC =4cm, BC = 6cm. Kẻ tia Cx vuông góc với BC (tia Cx và điểm A khác phía so với đường thẳng BC). Lấy trên Cx điểm D sao cho BD =9cm. Chứng minh rằng BD // AC

Xem đáp án

Lời giải

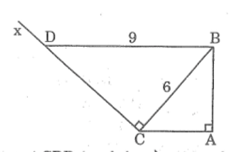
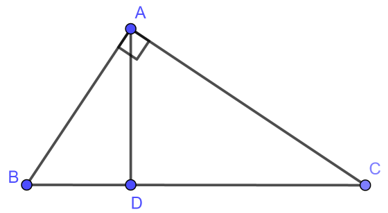
Xét hai tam giác vuông ABC và CDB, ta có:

$∠$ (BAC) = $∠$ (DCB) = $90^{0}$ (1)

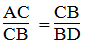
Mà: Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Suy ra: Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8 (2)

Từ (1) và (2) suy ra: $△$ ABC đồng dạng $△$ CDB (cạnh huyền và cạnh góc vuông tỉ lệ)

Suy ra: $∠$ (ACB) = $∠$ (CBD)

⇒ BD//AC ( hai góc ở vị trí so le trong bằng nhau )

Câu 2

Cho tam giác ABC vuông tại A, AC = 9cm, BC = 24cm. Đường trung trực của BC cắt đường thẳng AC tại D, cắt BC tại M. Tính độ dài của đoạn thẳng CD.

Xem đáp án

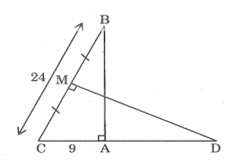
Lời giải

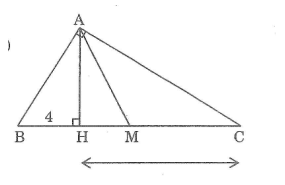
Xét hai tam giác vuông ABC và MDC, ta có:

$∠$ (BAC) = $∠$ (DMC ) = $90^{0}$

$∠$ C chung

Suy ra tam giác ABC đồng dạng với tam giác MDC (g.g)

Suy ra: Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Suy ra: Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Ta có: MC = 1/2 .BC = 1/2 .24 = 12 (cm)

Vây DC = (12.24)/9 = 32 (cm)

Câu 3

Đường cao của một tam giác vuông xuất phát từ đỉnh góc vuông chia cạnh huyền thành hai đoạn thẳng có dộ dài là 9cm và 16cm; Tính độ dài các cạnh của tam giác vuông.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Tam giác vuông ABC (A = $90^{0}$ ) có đường cao AH và trung tuyến AM. Tính diện tích tam giác AMH,biết rằng BH = 4cm, CH = 9cm

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho tam giác ABC ( $∠$ A = $90^{0}$ ) có đường cao AH. Chứng minh rằng $A H^{2} = B H . C H$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho tam giác ABC vuông tại A, chân H của đường cao AH chia cạnh huyền BC thành hai đoạn có độ dài 4cm và 9cm.
Gọi D và E là hình chiếu của H trên AB và AC.
Các đường thẳng vuông góc với DE tại D và E cắt BC theo thứ tự tại M và N . Chứng minh M là trung điểm của BH , N là trung điểm của CH.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Khóa học 1 - 12

THPT

THCS

Phòng luyện đề

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ô Ôn vào 10

Ôn vào 6

Ô Ôn vào 6

Tài liệu

THPT

THCS

Tin Tuyển Sinh