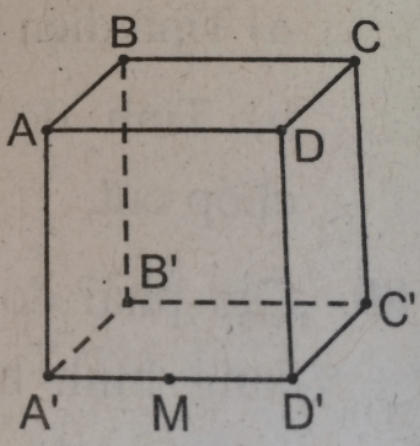
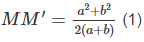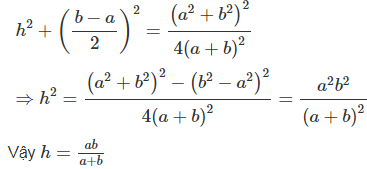Một con kiến đang ở vị trí M là trung điểm cạnh A'D' của một chiếc hộp hình lập phương ABCD.A'B'C'D' (h. bs.16). Con kiến muốn bò qua sáu mặt của chiếc hộp rồi quay trở về M. Tìm đường đi ngắn nhất của con kiến.
Câu hỏi trong đề: Giải Sách Bài Tập Toán 8 Tập 2 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
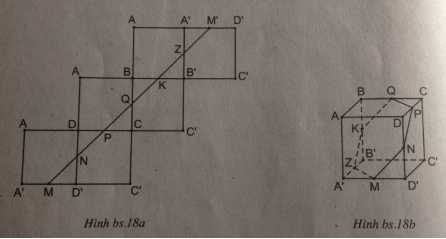
Trải 6 mặt của hình lập phương ABCD.A'B'C'D' như hình bs.18a. Để đi đường ngắn nhất từ M đến M' (M' chính là trung điểm của A'D' trên mặt khai triển) thì con kiến cần bò theo đoạn thẳng MM'. Trên chiếc hộp, đường đi ngắn nhất của con kiến là đường MNPQKZM' như ở hình bs.18b (dễ thấy N, P, Q, K, Z lần lượt là trung điểm của DD', CD, BC, BB', A'B').
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Ta có: V = 1/3 .S.h mà V = 126 () ,h = 6cm nên :
126 = 1/3 .S.6 ⇒ S = 126 :2 = 63 ()
Vậy chọn đáp án C
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
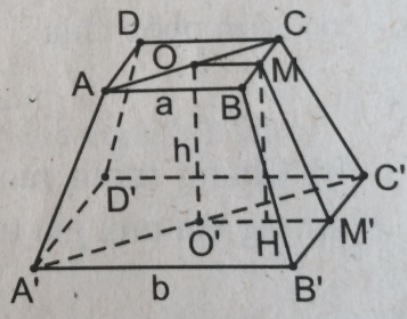
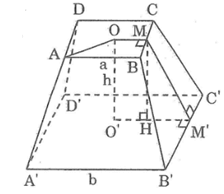
Xét hình chóp cụt đều ABCD.A'B'C'D' như hình bs.19.
Gọi M, M' thứ tự là trung điểm của BC, B'C'. Khi đó MM' là đường cao của hình thang cân BCC'B'.
Do đó diện tích xung quanh của hình chóp cụt đều là:
= 4.(a+b)/2.MM′=(2a+2b).MM′
Từ giả thiết ta có:
(2a+2b).MM′= 
Dễ thấy OM // O'M' nên OM và O'M' xác định mặt phẳng (OMM'O'). Trong mặt phẳng (OMM'O'), kẻ MH ⊥ O'M'. Khi đó: HM' = O'M' – O'H = (b−a)/2
Trong tam giác vuông MHM' ta có: (2)
Từ (1) và (2) suy ra :
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập