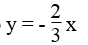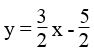Hãy kiểm tra xem mỗi cặp số sau có phải là một nghiệm của hệ phương trình tương ứng hay không?
(1,5; 2), (3; 7)
Câu hỏi trong đề: Giải Sách Bài Tập Toán 9 Tập 2 !!
Quảng cáo
Trả lời:
* Thay x = 1,5, y = 2 vào từng phương trình của hệ:
10.1,5 – 3.2 = 15 – 6 = 9
-5.1,5 + 1,5.2 = -7,5 + 3 = -4,5
Vậy (1,5; 2) là nghiệm của hệ phương trình
* Thay x = 3, y = 7 vào từng phương trình của hệ:
10.3 – 3.7 = 30 – 21 = 9
-5.3 + 1,5.7 = -15 + 10,5 = -4,5
Vậy (3; 7) là nghiệm của hệ phương trình
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
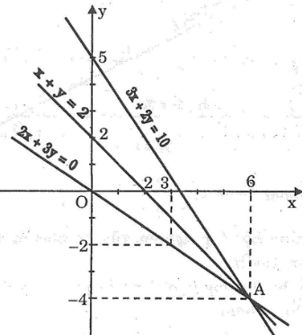
Vẽ đường thẳng () là đồ thị hàm số y = -x + 2
Cho x = 0 thì y = 2 ⇒ (0; 2)
Cho y = 0 thì x = 2 ⇒ (2; 0)
Vẽ đường thẳng () là đồ thị hàm số
Cho x = 0 thì y = 0 ⇒ (0; 0)
Cho x = 3 thì y = -2 ⇒ (3; -2)
Hai đường thẳng () và () cắt nhau tại A(6; -4). Thay các giá trị x và y này vào phương trình đường thẳng (), ta có:
3.6 + 2.(-4) = 18 – 8 = 10.
Vậy x và y thỏa phương trình 3x + 2y = 10 nên (x; y) = (6; -4) là nghiệm của phương trình 3x + 2y = 10.
Lời giải
Ta có: 3x – 2y = 5 ⇔
Để được một hệ có nghiệm duy nhất thì cần thêm một phương trình bậc nhất hai ẩn có hệ số góc khác 3/2 .
Chẳng hạn: 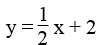
Khi đó ta có hệ 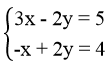
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.