2. Tốt nghiệp THPT
  3. Toán

Câu hỏi:

16/05/2020 1,074

Cho hình chóp S.ABC. Bên trong tam giác ABC ta lấy một điểm O bất kỳ. Từ O ta dựng các đường thẳng lần lượt song song với SA, SB, SC và cắt các mặt phẳng SBC,SCA,SAB theo thứ tự tại các điểm A’ , B’ , C’ . Tính tổng tỉ số T=OA'SA+OB'SB+OC'SC. 

Đáp án chính xác
Xem lời giải

Câu hỏi trong đề: Tuyển chọn đề thi thử thpt quốc gia môn Toán hay nhất có lời giải chi tiết !!

Bắt đầu thi Lưu câu hỏi

Quảng cáo

Trả lời:

verified
Giải bởi Vietjack

Đáp án C

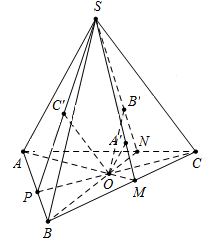
Gọi M,N,P lần lượt là giao điểm của OA, OB, OC với cạnh BC, CA, AB.

 Vì OB'//SA⇒OA'SA=OMAM (Định lí Thalet).

Tương tự, ta có OB'SB=ONBN';OC'SC=OPPC⇒T=OMAM+ONBN+OPPC. 

Với O là trọng tâm của tam giác ABC ⇒M,N,P lần lượt là trung điểm của BC, CA, AB

⇒OMAM=ONBN=OPCP=13. Vậy tổng tỉ số T=OA'SA+OB'SB+OC'SC=1. 

Chú ý: Bản chất bài toán là yêu cầu chứng minh OMAM+ONBN+OPPC=1. Tuy nhiên với tinh thần trắc nghiệm ta sẽ chuẩn hóa với O là trọng tâm tam giác ABC.

Sách thầy cô Vietjack biên soạn
Xem thêm »

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

  1. 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
  2. 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
  3. Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
  4. Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )

Bình luận


Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Chọn phát biểu sai trong các phát biểu sau

Xem đáp án » 16/05/2020 17,975

Câu 2:

Tìm khẳng định đúng trong các khẳng định sau.

Xem đáp án » 15/05/2020 15,176

Câu 3:

Cho hàm số y=fx có bảng biến thiên như sau.

Đồ thị hàm số y=fx−2017+2018 có bao nhiêu điểm cực trị?

Xem đáp án » 15/05/2020 10,473

Câu 4:

Cho hàm số y=lnx2−3x. Tập nghiệm S của phương trình f'x=0 là:

Xem đáp án » 15/05/2020 6,845

Câu 5:

Đường thẳng y=4x-1 và đồ thị hàm số y=x3−3x2−1 có bao nhiêu điểm chung?

Xem đáp án » 16/05/2020 5,164

Câu 6:

Cho hàm số fx liên tục trên đoạn a;b và có đạo hàm trên khoảng a;b 

Cho các khẳng định sau:

i) Tồn tại một số c∈a;b sao cho f'c=fb−fab−a. 

ii) Nếu fa=fb thì luôn tồn tại c∈a;b sao cho f'c=0. 

iii) Nếu fx có hai nghiệm phân biệt thuộc khoảng a;b thì giữa hai nghiệm đó luôn tồn tại một nghiệm của phương trình f'x=0. 

Số khẳng định đúng trong ba khẳng định trên là

Xem đáp án » 16/05/2020 4,830

Câu 7:

Đạo hàm của hàm số fx=lnlnx trên tập xác định của nó là:

Xem đáp án » 15/05/2020 4,681
Xem thêm các câu hỏi khác »
Hỏi bài tập
Vietjack official store
Đăng ký gói thi VIP

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

  • Được thi tất cả các đề của các lớp có trên Khoahoc.vietjack.com
  • Ngân hàng câu hỏi trắc nghiệm theo các mức độ Nhận biết, Thông hiểu, Vận dụng, Vận dụng cao.
  • Luyện chuyên sâu, rèn tốc độ với trọn bộ đề thi thử, đề minh họa, chính thức các năm.
  • Hỏi bài tập với đội ngũ chuyên môn cao của chúng tôi.

Đặt mua

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

  • Được thi tất cả các đề của các lớp có trên Khoahoc.vietjack.com
  • Ngân hàng câu hỏi trắc nghiệm theo các mức độ Nhận biết, Thông hiểu, Vận dụng, Vận dụng cao.
  • Luyện chuyên sâu, rèn tốc độ với trọn bộ đề thi thử, đề minh họa, chính thức các năm.
  • Hỏi bài tập với đội ngũ chuyên môn cao của chúng tôi.

Đặt mua

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

  • Được thi tất cả các đề của các lớp có trên Khoahoc.vietjack.com
  • Ngân hàng câu hỏi trắc nghiệm theo các mức độ Nhận biết, Thông hiểu, Vận dụng, Vận dụng cao.
  • Luyện chuyên sâu, rèn tốc độ với trọn bộ đề thi thử, đề minh họa, chính thức các năm.
  • Hỏi bài tập với đội ngũ chuyên môn cao của chúng tôi.

Đặt mua

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

  • Siêu tiết kiệm - Được thi tất cả các đề của các lớp có trên Khoahoc.vietjack.com
  • Ngân hàng câu hỏi trắc nghiệm theo các mức độ Nhận biết, Thông hiểu, Vận dụng, Vận dụng cao.
  • Luyện chuyên sâu, rèn tốc độ với trọn bộ đề thi thử, đề minh họa, chính thức các năm.
  • Hỏi bài tập với đội ngũ chuyên môn cao của chúng tôi.

Đặt mua

🔥 Đề thi HOT:

  1. 6372 người thi tuần này

    30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
  2. 4061 người thi tuần này

    (2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
  3. 1333 người thi tuần này

    Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
  4. 909 người thi tuần này

    CÂU TRẮC NGHIỆM ĐÚNG SAI
  5. 776 người thi tuần này

    (2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
  6. 616 người thi tuần này

    Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
  7. 511 người thi tuần này

    Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
  8. 443 người thi tuần này

    45 bài tập Xác suất có lời giải

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack72. All Rights Reserved.

Đăng ký

Bạn đã có tài khoản?