Tổng hợp đề thi THPT Quốc gia có lời giải chi tiết (Đề số 2)
79 người thi tuần này 4.6 3 K lượt thi 50 câu hỏi 90 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Nguyễn Thị Minh Khai (Hà Nội) lần 1 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Liên trường THPT (Nghệ An) có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Chuyên Đại học Vinh lần 1 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Cụm liên trường Nghệ An có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Sở Bắc Ninh có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Chuyên ĐH KHTN Hà Nội lần 1 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Sở Hưng Yên có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Nguyễn Gia Thiều (Hà Nội) có đáp án
Danh sách câu hỏi:
Lời giải
Đáp án D
Ta có:
Số tập con gồm k phần tử của A là: thì nhỏ nhất.
Lời giải
Đáp án A
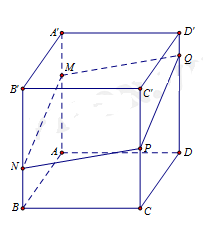
Ta chứng minh được công thức tỷ số thể tích tối với khối hộp như sau (học sinh có thể tự chứng minh).
Khi đó:
Lời giải
Đáp án C
Số hạng tổng quát là: bắt đầu từ số hạng thứ thì nhận giá trị âm.
Lời giải
Đáp án C
TXĐ:
Ta có: là TCĐ.
Không tồn tại nên đồ thị hàm số không có tiệm cận ngang.
Lời giải
Đáp án A
Điều kiện:
Ta có:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A.
B.
C.
D. X là trung điểm của đoạn AB
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
A. Nếu một đường thẳng song song với một mặt phẳng thì nó song song với một đường thẳng nào đó nằm trong mặt phẳng đó.
B. Nếu hai mặt phẳng cùng song song với mặt phẳng thứ ba thì chúng song song với nhau.
C. Nếu ba mặt phẳng phân biệt đôi một cắt nhau theo ba giao tuyến thì ba giao tuyến đó phải đồng quy.
D. Trong không gian, hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì hai đường thẳng đó song song với nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A.
B.
C. a cũng là nghiệm của phương trình
D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
A. Hàm số chỉ có một điểm cực trị.
B. Đồ thị của hàm số nhận trục tung làm trục đối xứng.
C. Hàm số đã cho là hàm số chẵn.
D. Các điểm cực trị của đồ thị hàm số tạo thành một tam giác cân
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
A. Đoạn thẳng nối trung điểm của cặp cạnh đối diện cũng là đoạn vuông góc chung của cặp cạnh đó
B. Thể tích của tứ diện bằng một phần ba tích khoảng cách từ trọng tâm của tứ diện đến một mặt với diện tích toàn phần của nó (diện tích toàn phần là tổng diện tích của bốn mặt).
C. Các cặp cạnh đối diện dài bằng nhau và vuông góc với nhau.
D. Hình tứ diện đều có một tâm đối xứng cũng chính là trọng tâm của nó.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 27
A. Đồ thị hàm số có đường tiệm cận ngang
B. Điểm cực đại của đồ thị hàm số
C. Hàm số đồng biến trên các khoảng
D. Hàm số không có cực trị.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 31
A. Hàm số đạt cực trị tại điểm thì đạo hàm tại đó không tồn tại hoặc
B. Hàm số có , thì hàm số đồng biến trên
C. Hàm số đồng biến trên đoạn thì đạt giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.
D. Hàm số liên tục trên đoạn và thì tồn tại sao cho
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 34
A. Khối tứ diện đều đối ngẫu với chính nó.
B. Hai khối đa diện đều đối ngẫu với nhau luôn có số cạnh bằng nhau.
C. Số mặt của một đa diện đều bằng số cạnh của đa diện đều đối ngẫu với nó.
D. Khối 20 mặt đều đối ngẫu với khối 12 mặt đều.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 36
A. Dãy số có tất cả các số hạng bằng nhau là một cấp số cộng.
B. Một cấp số nhân có công bội là một dãy tăng.
C. Dãy số có tất cả các số hạng bằng nhau là một cấp số nhân.
D. Một cấp số cộng có công sai dương là một dãy tăng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 47
A. Nếu hai mặt phẳng song song cùng cắt mặt phẳng thứ ba thì hai giao tuyến tạo thành song song với nhau
B. Ba mặt phẳng đôi một song song chắn trên hai đường thẳng chéo nhau những đoạn thẳng tương ứng tỉ lệ
C. Nếu mặt phẳng (P) song song với mặt phẳng (Q) thì mọi đường thẳng nằm trên mặt phẳng (P) đều song song với mặt phẳng (Q).
D. Nếu mặt phẳng (P) có chứa hai đường thẳng phân biệt và hai đường thẳng đó cùng song song với mặt phẳng (Q) thì mặt phẳng (P) song song với mặt phẳng (Q).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 50
A. Một mặt phẳng đi qua S.
B. Một mặt cầu đi qua S.
C. Một mặt nón có đỉnh là S.
D. Một mặt trụ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

