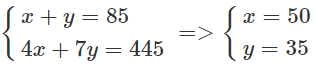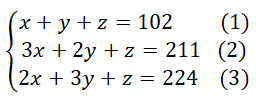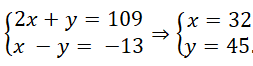Một chủ cửa hàng bán lẻ mang 1 500 000 đồng đến ngân hàng đổi tiền để trả lại cho người mua. Ông ta đổi được tất cả 1 450 đồng tiền xu các loại 2000 đồng, 1000 đồng và 500 đồng. Biết rằng số tiền xu loại 1 000 đồng bằng hai lần hiệu của số tiền xu loại 500 đồng với số tiền xu loại 2000 đồng. Hỏi mỗi loại có bao nhiêu đồng tiền xu?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi x, y, z lần lượt là số đồng tiền xu loại 2000 đồng, 1000 dồng, 500 đồng.
Điều kiện là x, y, z nguyên dương
Ta có hệ phương trình
x + y + z = 1450 (1)
4x + 2y + z = 3000 (2)
2x + y - 2z = 0 (3)
Trừ từng vế tương ứng của phương trình (2) với phương trình (1) ta được
3x + y = 1550
Cộng từng vế tương ứng của các phương trình (1), (2) và (3) ta có :
7x + 4y = 4450.
Giải hệ gồm hai phương trình (4) và (5) ta được.
x = 350, y = 500.
Thay các giá trị của x, y vào phương trình (1) ta được z = 600.
Vậy cửa hàng đổi được 350 đồng tiền xu loại 2000 đồng, 500 đồng tiền loại 1000 đồng và 600 đồng tiền xu loại 500 đồng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi x là số xe 4 chỗ, y là số xe 7 chỗ. Điều kiện x và y nguyên dương.
Ta có hệ phương trình.
thỏa mãn điều kiện của bài toán).
Vậy công ty có 50 xe 4 chỗ và 35 xe 7 chỗ.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi x là số phòng 3 người, y là số phòng 2 người, z là số phòng 1 người, ta được hệ phương trình
Cách 1. Dùng máy tính cầm tay.
Cách 2. Khử z để đưa về hệ phương trình hai ẩn. Trừ vế theo vế phương trình (2) cho phương trình (1) và phương trình (2) cho phương trình (3) ta được hệ phương trình
Từ đó thay vào (1) ta được z = 25.
Vậy đáp án là B.
Cách 3. Tính nhẩm.
Với phương án A, vế trái của phương trình (2) bằng 243 nên bị loại. Với phương án C, vế trái của phương trình (3) bằng 245 nên bị loại. Tương tự với phương án D, vế trái của phương trình (3) bằng 245 nên loại.
Đáp án: B
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập