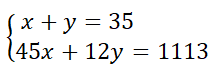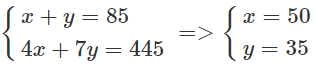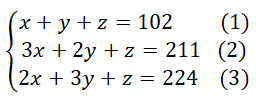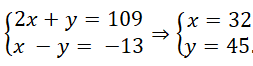Một công ti kinh doanh xe buýt có 35 xe gồm hai loại: loại xe chở được 45 khách và loại xe chở được 12 khách. Nếu dùng tất cả số xe đó tối đa công ti chở một lần được 1113 khách. Vậy công ti có số xe mỗi loại là:
    A. 20 xe 45 chỗ, 15 xe 12 chỗ.
    B. 17 xe 45 chỗ, 18 xe 12 chỗ.
    C. 21 xe 45 chỗ, 14 xe 12 chỗ.
    D. 19 xe 45 chỗ, 16 xe 12 chỗ.

Xem lời giải

Câu hỏi trong đề: Giải sbt Đại số 10 Bài 3: Phương trình và hệ phương trình bậc nhất nhiều ẩn !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Gọi x là số xe chở được 45 khách, y là số xe chở được 12 khách. Ta có hệ phương trình

Giải sách bài tập Toán 10 | Giải sbt Toán 10

Nếu dùng máy tính cầm tay, ta nhập hệ phương trình vào máy, sẽ cho ngay kết quả là phương án C.

Nếu không dùng máy tính, ta có thể xét các phương án, với nhận xét là số xe 45 chỗ càng nhiều thì tổng số khách trở được càng lớn. Bắt đầu từ phương án A vì có số xe 45 chỗ là 20 dễ tính nhẩm, ta được tổng số khách chở được là 1080, ít hơn số 1113, nên phương án A bị loại. Các phương án B và D có số xe 45 chỗ ít hơn 20 nên số khách chở được càng ít hơn, nên B và D cũng bị loại.

Đáp án: C

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một công ti có 85 xe chở khách gồm hai loại, xe chở được 4 khách và xe chở được 7 khách. Dùng tất cả số xe đó, tối đa công ti chở một lần được 445 khách. Hỏi công ti đó có mấy xe mỗi loại?

Xem đáp án

Lời giải

Gọi x là số xe 4 chỗ, y là số xe 7 chỗ. Điều kiện x và y nguyên dương.

Ta có hệ phương trình.

Giải sách bài tập Toán 10 | Giải sbt Toán 10

thỏa mãn điều kiện của bài toán).

Vậy công ty có 50 xe 4 chỗ và 35 xe 7 chỗ.

Câu 2

Một khách sạn có 102 phòng gồm ba loại: phòng 3 người, phòng 2 người và phòng 1 người. Nếu đầy khách tất cả các phòng thì khách sạn đón được 211 khách. Còn nếu cải tạo lại các phòng bằng cách: sửa các phòng 2 người thành 3 người, còn phòng 3 người sửa lại thành phòng 2 người và giữ nguyện phòng 1 người thì tối đa một lần có thể đón 224 khách.
    Vậy số phòng từng loại hiện nay của khách sạn là:
    A. 50 phòng 3 người, 41 phòng 2 người, 11 phòng 1 người.
    B. 32 phòng 3 người, 45 phòng 2 người, 25 phòng 1 người.
C. 41 phòng 3 người, 51 phòng 2 người, 10 phòng 1 người.
    D. 25 phòng 3 người, 59 phòng 2 người, 18 phòng 1 người.

Xem đáp án

Lời giải

Gọi x là số phòng 3 người, y là số phòng 2 người, z là số phòng 1 người, ta được hệ phương trình

Giải sách bài tập Toán 10 | Giải sbt Toán 10

Cách 1. Dùng máy tính cầm tay.

Cách 2. Khử z để đưa về hệ phương trình hai ẩn. Trừ vế theo vế phương trình (2) cho phương trình (1) và phương trình (2) cho phương trình (3) ta được hệ phương trình

Giải sách bài tập Toán 10 | Giải sbt Toán 10

Từ đó thay vào (1) ta được z = 25.

Vậy đáp án là B.

Cách 3. Tính nhẩm.

Với phương án A, vế trái của phương trình (2) bằng 243 nên bị loại. Với phương án C, vế trái của phương trình (3) bằng 245 nên bị loại. Tương tự với phương án D, vế trái của phương trình (3) bằng 245 nên loại.

Đáp án: B

Câu 3