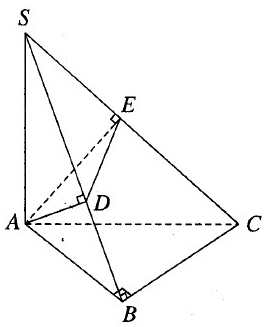
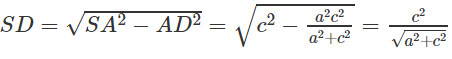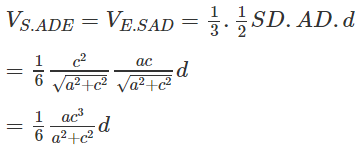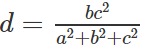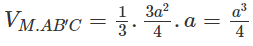Cho hình chóp tam giác S.ABC có đáy là tam giác vuông ở B. Cạnh SA vuông góc với đáy. Từ A kẻ các đoạn thẳng AD vuông góc với SB và AE vuông góc với SC. Biết rằng AB = a, BC = b, SA = c. Tính khoảng cách từ E đến mặt phẳng (SAB).
Quảng cáo
Trả lời:
Gọi d là khoảng cách từ E đến mặt phẳng (SAB)
Ta có:
Kết hợp với kết quả trong câu a)
ta suy ra
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
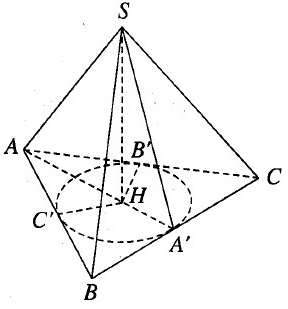
Kẻ SH (ABC) và HA’, HB’ , HC’ lần lượt vuông góc với BC, CA, AB. Theo định lí ba đường vuông góc ta có SA′ BC, SB′ CA, SC′ AB
Từ đó suy ra SA′H = SB′H = SC′H = 60.
Do đó các tam giác vuông SHA’ , SHB’ , SHC’ bằng nhau. Từ đó suy ra HA’ = HB’ = HC’ . Vậy H là tâm đường tròn nội tiếp tam giác ABC. Do tam giác cân ở A nên AH vừa là đường phân giác , vừa là đường cao, vừa là đường trung tuyến. Từ đó suy ra A, H, A’ thẳng hàng và A’ là trung điểm của BC.
Do đó,
Vậy AA’ = 4a
Gọi p là nửa chu vi của tam giác ABC, r là bán kính đường tròn nội tiếp của nó.
Khi đó SABC = 6a.4a/2 = 12a2 = pr = 8ar
Từ đó suy ra r = 3a/2
Do đó
Thể tích khối chóp là:
Lời giải
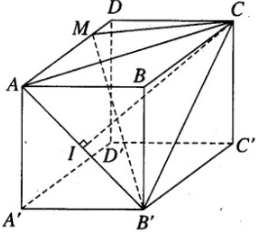
Thể tích khối chóp M.AB’C bằng thể tích khối chóp B’AMC. Ta có:
Do đó
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.