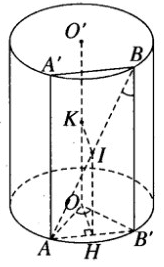
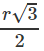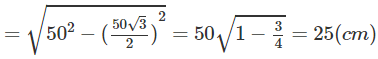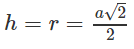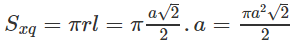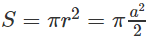Một khối trụ có bán kính đáy bằng r và chiều cao bằng r. Gọi A và B là hai điểm trên hai đường tròn đáy sao cho góc được tạo thành giữa đường thẳng AB và trục của khối trụ bằng 30. Xác định và tính độ dài đoạn vuông góc chung của AB và trục của khối trụ.
Câu hỏi trong đề: Giải SBT Toán 12 Bài 1: Khái niệm về mặt tròn xoay !!
Quảng cáo
Trả lời:
Mặt phẳng (ABB’) chứa AB và song song với trục OO’ của hình trụ. Gọi H là trung điểm của AB’. Ta có OH (ABB′). Đường thẳng qua H song song với OO’ cắt AB tại I. Dựng IK // HO cắt OO’ tại K. Ta chứng minh được IK là đoạn vuông góc chung của AB và OO’.
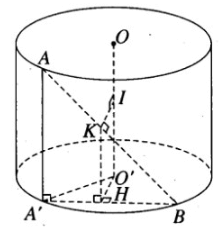
Ta có: IK = HO =
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Giả sử đoạn thẳng AB có điểm mút A nằm trên đường tròn đáy tâm O’ . Theo giả thiết ta có: AB = 100 cm. Giả sử IK là đoạn vuông góc chung của trục OO’ và đoạn AB với I thuộc OO’ và K thuộc AB. Chiếu vuông góc đoạn AB xuống mặt phẳng đáy chứa đường tròn tâm O’ , ta có A’ , H , B lần lượt là hình chiếu của A, K, B.
Vì KI OO′ nên IK // mp(O’BA’) , do đó O’H // IK và O’H = IK.
Ta suy ra O′H AB và O′H AA′. Vậy O′H A′B
Xét tam giác vuông AA’B ta có
Vậy
Lời giải
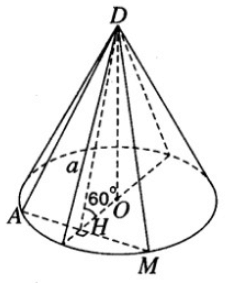
Thiết diện qua trục của hình nón là tam giác vuông cân cạnh a nên hình nón có đường sinh l = a,
có bán kính đáy
và có chiều cao
Gọi là diện tích xung quanh của hình nón, ta có:
Gọi S là diện tích đáy của hình nón, ta có
Vậy diện tích toàn phần của hình nón đã cho là:
Hình nón có thể tích là:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.