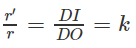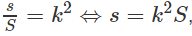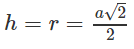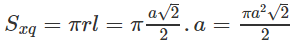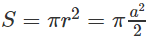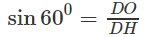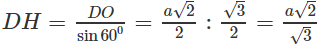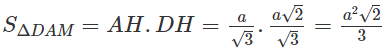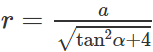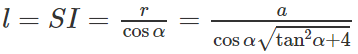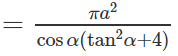Bài 1: Khái niệm về mặt tròn xoay
34 người thi tuần này 4.6 1.2 K lượt thi 19 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
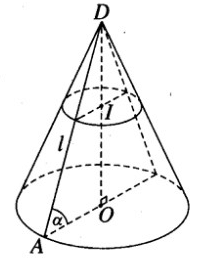
Gọi r là bán kính của đường tròn đáy.
Ta có OA = r = l.cos (với O là tâm của đường tròn đáy và A là một điểm trên đường tròn đó).
Ta suy ra:
Khối nón có chiều cao h = DO = lsin. Do đó thể tích V của khối nón được tính theo công thức
Vậy :
Lời giải
Thiết diện qua I và vuông góc với trục hình nón là một hình tròn bán kính r’
với
Gọi s là diện tích của thiết diện và S là diện tích của đáy hình tròn ta có:
trong đó S =
Vậy diện tích của thiết diện đi qua điểm I và vuông góc với trục hình nón là: s =
Lời giải
Thiết diện qua trục của hình nón là tam giác vuông cân cạnh a nên hình nón có đường sinh l = a,
có bán kính đáy
và có chiều cao
Gọi là diện tích xung quanh của hình nón, ta có:
Gọi S là diện tích đáy của hình nón, ta có
Vậy diện tích toàn phần của hình nón đã cho là:
Hình nón có thể tích là:
Lời giải
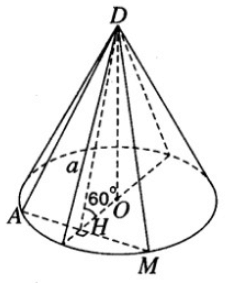
Xét mặt phẳng (DAM) đi qua đỉnh D tạo với mặt phẳng đáy một góc 600, cắt đường tròn đáy tại hai điểm A và M. Từ tâm O của đường tròn đáy ta vẽ OH AM, do vậy H là trung điểm của đoạn AM. Ta có AM (DOH) vì AM OH và AM DO.
Vậy DHO = 60 và
hay
Gọi SΔ DAM là diện tích thiết diện cần tìm, ta có: = AH.DH
Mà
Vậy
Lời giải
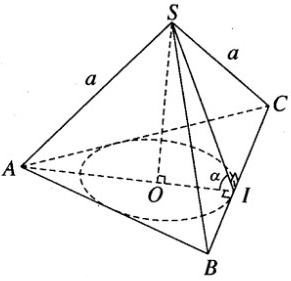
Gọi I là trung điểm của cạnh BC và O là tâm của tam giác đều ABC. Theo giả thiết ta có SA = SB = SC = a và SIO = α. Đặt OI = r, SO = h, ta có AO = 2r và
Do đó
Vậy
Hình nón nội tiếp có đường sinh là :
Diện tích xung quanh của hình nón nội tiếp hình chóp S.ABC là:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.