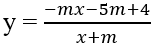Giải sbt Giải tích 12 Bài 1: Sự đồng biến, nghịch biến của hàm số
30 người thi tuần này 4.6 1.5 K lượt thi 16 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
a) TXĐ: R
y′ = 6x − 24 = 6x(1 − 4x)
y' = 0 ⇔
y' > 0 trên khoảng (0; 1/4) , suy ra y đồng biến trên khoảng (0; 1/4)
y' < 0 trên các khoảng (; 0 ); (14; ), suy ra y nghịch biến trên các khoảng (;0 ); (14;)
b) TXĐ: R
y′ = 16 + 4x − 16 − 4 = −4(x + 4)( − 1)
y' = 0 ⇔
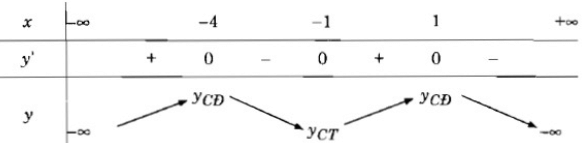
Bảng biến thiên:
Vậy hàm số y đã cho đồng biến trên các khoảng (; -4) và (-1; 1), nghịch biến trên các khoảng (-4; -1) và (1;)
c) TXĐ: R
y′ = 3 − 12x + 9
y' = 0
y' > 0 trên các khoảng (; 1), (3; ) nên y đồng biến trên các khoảng (; 1), (3; )
y'< 0 trên khoảng (1; 3) nên y nghịch biến trên khoảng (1; 3)
d) TXĐ: R
y′ = 4 + 16 = 4x( + 4)
y' = 0 ⇔
y' > 0 trên khoảng (0; ) ⇒ y đồng biến trên khoảng (0; )
y' < 0 trên khoảng (; 0) ⇒ y nghịch biến trên khoảng (; 0)
Lời giải
a) TXĐ: R \ {-7}
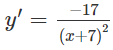
y' < 0 trên các khoảng (; -7), (-7; ) nên hàm số nghịch biến trên các khoảng đó
b) TXĐ: R \ {5}
![]()
y' < 0 trên khoảng (5; ) nên y nghịch biến trên khoảng (5; )
y' > 0 trên khoảng (; 5) nên y đồng biến trên khoảng (; 5)
c) TXĐ: R \ {-3; 3}
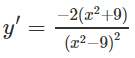
y' < 0 trên các khoảng (; - 3), (-3; 3), (3; ) nên hàm số đã cho nghịch biến trên các khoảng đó.
d) TXĐ: R \ {0}
![]()
y' = 0 ⇔
Bảng biến thiên:
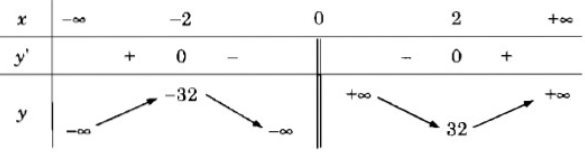
Vậy hàm số đã cho đồng biến trên các khoảng (-∞; -2), (2; +∞) và nghịch biến trên các khoảng (-2; 0), (0; 2)
e) TXĐ: R \ {-1}
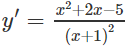
y' = 0 ⇔
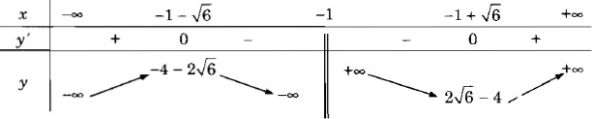
Vậy hàm số đã cho đồng biến trên các khoảng (; −1 − √6), (−1 + √6; ) và nghịch biến trên các khoảng (−1 − √6; −1),(−1; −1 + √6)
g) TXĐ: R \ {2}
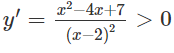
(do x2 − 4x + 7x2 − 4x + 7 có Δ' = - 3 < 0)
Vậy hàm số đã cho đồng biến trên các khoảng (−∞;2),(2;+∞)
Lời giải
a) TXĐ: [0; +∞)
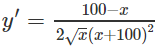
y’ = 0 ⇔ x = 100
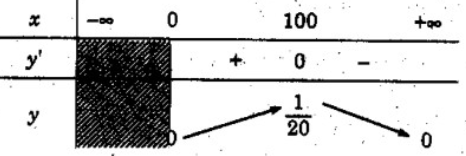
Vậy hàm số đồng biến trên khoảng (0; 100) và nghịch biến trên khoảng (100; )
b) TXĐ: (; √6) ∪ (√6; )
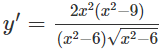
y’ = 0 ⇔ x = 3 hoặc x = -3
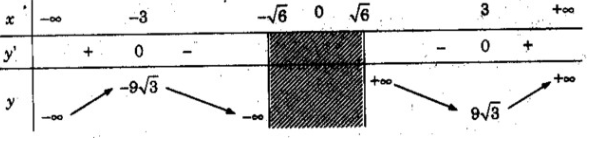
Vậy hàm số đồng biến trên các khoảng (; -3), (3; ), nghịch biến trên các khoảng (-3; −√6 − 6 ), (√6; 3).
Lời giải
a) y = x – sinx, x ∈ [0; 2π].
y′ = 1 – cosx ≥ 0 với mọi x ∈ [0; 2π]
Dấu “=” xảy ra chỉ tại x = 0 và x = 2π.
Vậy hàm số đồng biến trên đoạn [0; 2π].
c) Xét hàm số y = sin(1/x) với x > 0.
![]()
Giải bất phương trình sau trên khoảng (0; ):
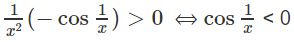
Do đó, hàm số đồng biến trên các khoảng
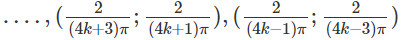
Và nghịch biến trên các khoảng
với k = 0, 1, 2 …
Lời giải
a) Tập xác định: D = R \ {m}
Hàm số đồng biến trên từng khoảng (; m), (m; ) khi và chỉ khi:
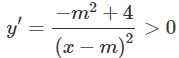
⇔ − + 4 > 0
⇔ < 4 ⇔ −2 < m < 2
c) Tập xác định: D = R
Hàm số nghịch biến trên R khi và chỉ khi:
y′ = −3 + 2mx – 3 ≤ 0
⇔ y′ = – 9 ≤ 0
⇔ ≤ 9 ⇔ −3 ≤ m ≤ 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
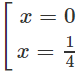
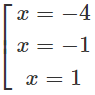
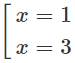
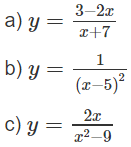
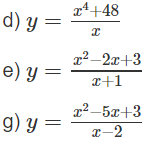
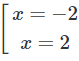
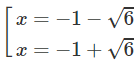
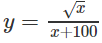
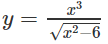
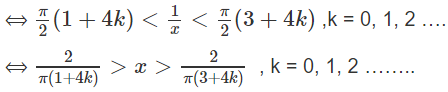
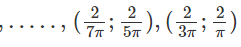
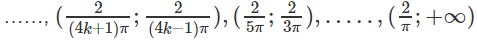
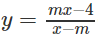 đồng biến trên từng khoảng xác định;
đồng biến trên từng khoảng xác định;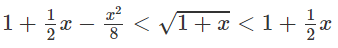
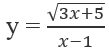 xác định trên R
xác định trên R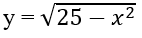 nghịch biến trên khoảng:
nghịch biến trên khoảng: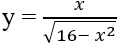 đồng biến trên khoảng:
đồng biến trên khoảng: