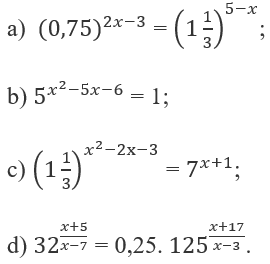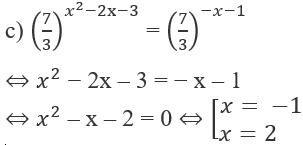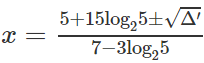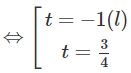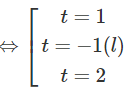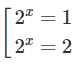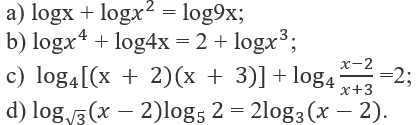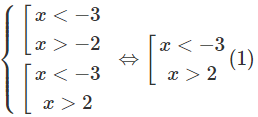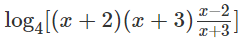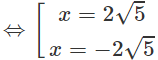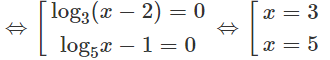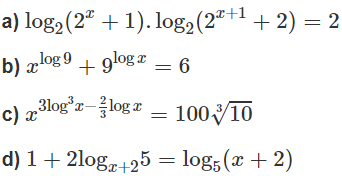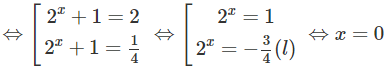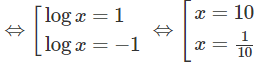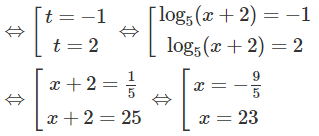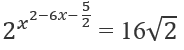Giải sbt Giải tích 12 Bài 5: Phương trình mũ và phương trình lôgarit
36 người thi tuần này 4.6 1.7 K lượt thi 13 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
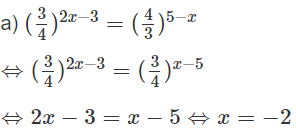
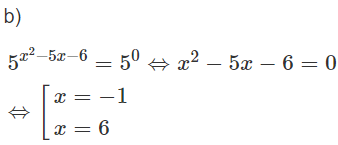
d) Hướng dẫn: Lấy logarit cơ số 2 cả hai vế
Phương trình đã cho có hai nghiệm phân biệt đều thỏa mãn điều kiện
Lời giải
a) 16. + 4. = 5. + 3.
⇔ 20.= 8. ⇔ (2/5)x = ⇔ x = 1
b) 16. − 16. = 0
⇔ = ⇔ = ⇔ x = 0
c) Chia hai vế cho ( > 0), ta được:
4 + 1 − 3 = 0
Đặt t = (t > 0), ta có phương trình:
4t + 1 − 3/t = 0 ⇔ 4 + t − 3 = 0
Do đó, = . Vậy x = 1.
d) Đặt t = (t > 0), ta có phương trình:
− + 2 + t – 2 = 0
⇔ (t − 1)(t + 1)(2 − t) = 0
Do đó:
Lời giải
a) Với điều kiện x > 0, ta có
logx + 2logx = log9 + logx
⇔ logx = log3 ⇔ x = 3
b) Với điều kiện x > 0, ta có
4logx + log4 + logx = 2log10 + 3logx
⇔ logx = log5 ⇔ x = 5
c) Ta có điều kiện của phương trình đã cho là:
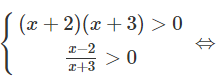
Khi đó, phương trình đã cho tương đương với:
= log416 ⇔ − 4 = 16
Cả hai nghiệm trên đều thỏa mãn điều kiện (1).
d) Với điều kiện x > 2, ta có phương trình
Cả hai giá trị này đều thỏa mãn điều kiện x > 2.
Lời giải
a) . = 2
⇔ . [1 + ] = 2
Đặt t = , ta có phương trình
t(1 + t) = 2 ⇔ + t – 2 = 0
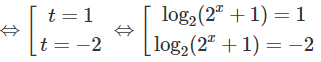
b) Với điều kiện x >0, ta có: log() = log()
log(xlog9) = log9.logx và log() = logx.log9
Nên log() = log()
Suy ra: =
Đặt t = , ta được phương trình 2t = 6 ⇔ t = 3 ⇔ = 3
⇔ log() = log3
⇔log9.logx = log3
⇔logx = log3/log9 ⇔ logx = 1/2
⇔ x = (thỏa mãn điều kiện x > 0)
c) Với điều kiện x > 0, lấy logarit thập phân hai vế của phương trình đã cho, ta được:
(3 − 2logx/3).logx = 7/3
Đặt t = logx, ta được phương trình 3 − 2/3 – 7/3 = 0
⇔ 9 − 2 − 7 = 0
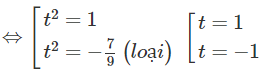
d) Đặt t = với điều kiện x + 2 > 0, x + 2 ≠ 1, ta có:
1 + 2/t = t ⇔ – t – 2 = 0 , t ≠ 0
Lời giải
Đáp án : B
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.