Cho hình chóp S.ABC có tam giác ABC vuông cân tại B, AB = a. Gọi I là trung điểm của AC. Hình chiếu vuông góc của S lên mặt phẳng (ABC) là điểm H thỏa mãn = 3. Góc giữa hai mặt phẳng (SAB) và (SBC) là 60 độ. Thể tích của khối chóp S.ABC là:
A. V = a3/9
B.V = a3/6
C.V = a3/18
D.V = a3/3
Câu hỏi trong đề: 80 câu trắc nghiệm Khối đa diện nâng cao !!
Quảng cáo
Trả lời:
Chọn A
Cách 1:
Dễ thấy hai tam giác SAB và SAC bằng nhau (cạnh chung SA), gọi K là chân đường cao hạ từ A trong tam giác SAB
Từ giả thiết tam giác ABC vuông cân tại B ta được
Trong tam giác ICK vuông tại I có .
Suy ra IK > IB.
Do nên tam giác BIK vuông tại K
Như vậy IK > IB (vô lý do IB là cạnh huyền).
TH2: tương tự phần trên ta có
Do nên tam giác BIK vuông tại K và
Như vậy tam giác BKI đồng dạng với tam giác BHS suy ra:
Vậy thể tích của khối chóp S.ABC là
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn C
Gọi M là trung điểm của BC
=> AM BC (1)
Ta có
Mặt khác
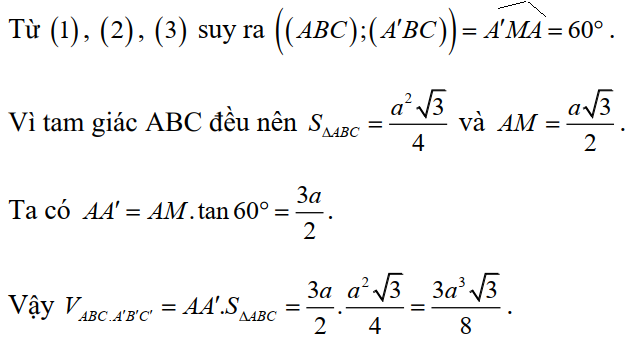
Lời giải
Chọn C
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Miea
Cho tứ diện SABC có tam giác ABC vuông cân tại B, SA vuông góc ( ABC ), cho SA = a√2 , AB = a. Gọi H , K lần lượt là chân đường vuông góc của A lên các cạnh SB , SC .
1 / Chứng minh :
a ) BC vuông góc ( SAB )
b ) AH vuông góc SC
c ) ( SAB ) vuông góc ( SBC )
d ) SC vuông góc( AHK )
2 / Tính góc giữa hai mặt phẳng :
a ) ( SBC ) và ( ABC )
b ) ( AHK ) và ( SAB )
3 / Tìm khoảng cách từ A đến ( SBC ) , khoảng cách từ B đến ( SAC )
4 / Tìm góc giữa :
a ) SB với ( ABC )
b ) SC với ( ABC )
c ) AH với ( ABC )