Câu hỏi:

12/07/2024 1,997

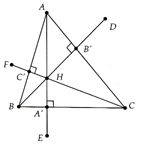
Cho tam giác ABC nhọn và H là trực tâm, các đường cao AA'; BB'; CC'. Lần lượt lấy đối xứng H qua BC, AC, AB được các điểm E, D, F. Chứng minh $\frac{H E}{A' A} + \frac{H D}{B' B} + \frac{H F}{C' C} = 2.$

Xem lời giải

Câu hỏi trong đề: Bài tập: Ôn tập chương II !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Chứng minh

HE = 2HA'; HD = 3HD'; HF = 2HS;

Theo kết quả trắc nghiệm có:

$\frac{H A'}{A A'} + \frac{H B'}{B B'} + \frac{H C'}{C C'} = 1;$

Nhân hai vế với 2 Þ ĐPCM

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác MNP vuông tại M, MN = 4 cm, NP = 5 cm. Diện tích tam giác MNP là

Xem đáp án

Lời giải

6 cm²

Câu 2

Cho tam giác ABC vuông tại A. AB = 7,5 cm; BC = 12,5cm.
          a) Tính diện tích tam giác ABC.
          b) Lấy điểm M trên cạnh AB sao cho AM: MB = 1:2. Từ M kẻ đường thẳng song song với BC cắt trung tuyến AF tại E và cắt cạnh AC tại N. Chứng minh E là trung điểm của MN.
          c) Gọi G, H, I thứ tự là trung điểm của MC, NB và FE. Chứng minh G, H, I thẳng hàng và tính diện tích ∆IHF

Xem đáp án

Lời giải

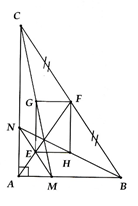
a) AC = 10cm Þ S_ABC =37,5 (cm²)

b) Chứng minh được $\hat{M A E} = \hat{A M E}$ (cùng = $\hat{A B C}$ ) Þ AE = ME. Cmtt ta có AE = NE. Từ đó suy ra ME = NE.

c) Chứng minh EH//GF (//MB) và GE//FH (//NC) Þ EGFH là hình bình hành. Chứng minh được $\hat{H E G} = \hat{B A C} = 90^{0} \Rightarrow E G F H$ là hình chữ nhật. Suy ra GH đi qua trung điểm của EF.

$S_{E G F H} = H E . E G = \frac{1}{2} M B . \frac{1}{2} N C = \frac{1}{4} . \frac{2}{3} A B . \frac{2}{3} A C = \frac{25}{3} (c m^{2})$

Mà $S_{E G F H} = 4. S {}_{I H F}\Rightarrow S_{I H F} = \frac{25}{12} c m^{2}$

Câu 3

Cho tam giác ABC nhọn. Các đường cao AA’, BB’, CC’ cắt nhau tại H. Tổng $\frac{H A'}{A A'} + \frac{H B'}{B B'} + \frac{H C'}{C C'}$ bằng?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho tam giác ABC đường trung tuyến AM . Kết quả nào sau đây là sai

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho tam giác PMN vuông tại N, E và F thứ tự là trung điểm của MN và MP. Gọi G là điểm đối xứng của F qua E. So sánh S_MNp và S_MGNF

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Một đa giác đều có tổng các góc trong bằng 1440°. Số cạnh của đa giác này là:

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Văn

Tiếng Anh

Cho tam giác ABC nhọn và H là trực tâm, các đường cao AA'; BB'; CC'. Lần lượt lấy đối xứng H qua BC, AC, AB được các điểm E, D, F. Chứng minh $\frac{H E}{A' A} + \frac{H D}{B' B} + \frac{H F}{C' C} = 2.$

Cho tam giác ABC nhọn. Các đường cao AA’, BB’, CC’ cắt nhau tại H. Tổng $\frac{H A'}{A A'} + \frac{H B'}{B B'} + \frac{H C'}{C C'}$ bằng?

Cho tam giác PMN vuông tại N, E và F thứ tự là trung điểm của MN và MP. Gọi G là điểm đối xứng của F qua E. So sánh S_MNp và S_MGNF