Chọn câu sai:
a) 11. + 16 chia hết cho 4 nên chia hết cho 2;
b) 24.8 – 17 chia hết cho 3;
c) 136.3 – 2. chia hết cho 9;
d) Tích của ba số tự nhiên liên tiếp chia hết cho 2, cho 3.
Quảng cáo
Trả lời:
Lời giải:
a) Phát biểu a) là đúng vì 11.+ 16 chia hết cho 4 mà 4 lại chia hết cho 2 nên 11. + 16 chia hết cho 2.
b) Vì 24 chia hết cho 3 nên 24.8 chia hết cho 3
Mà 17 không chia hết cho 3
Nên theo tính chất chia hết của một hiệu thì 24.8 – 17 không chia hết cho 3.
Do đó phát biểu b) sai.
c) Ta có: 2. = 2. = 2.9.9 chia hết cho 9;
Mà 136.3 không chia hết cho 9
Nên theo tính chất chia hết của một hiệu thì 136.3 – 2.34 không chia hết cho 9.
Do đó phát biểu c) là sai.
d) Gọi ba số tự nhiên liên tiếp là n, n + 1, n + 2 với n là số tự nhiên.
+) Quan hệ chia hết của n(n + 1)(n + 2) với 2
- Nếu n là số chẵn thì n chia hết cho 2. Suy ra n(n + 1)(n + 2) chia hết cho 2.
- Nếu n là số lẻ thì n + 1 là số chẵn nên n + 1 chia hết cho 2. Suy ra n(n + 1)(n + 2) chia hết cho 2.
Do đó n(n + 1)(n + 2) chia hết cho 2 với mọi số tự nhiên n (1).
+) Quan hệ chia hết của n(n + 1)(n + 2) với 3
- Nếu n chia hết cho 3 thì n(n + 1)(n + 2) chia hết cho 3.
- Nếu n chia cho 3 dư 1 thì n = 3k + 1 với k là số tự nhiên. Khi đó n + 2 = 3k + 3 = 3(k + 1) chia hết cho 3. Suy ra n(n + 1)(n + 2) chia hết cho 3.
- Nếu n chia cho 3 dư 2 thì n = 3k + 2 với k là số tự nhiên. Khi đó n + 1 = 3k + 3 = 3(k + 1) chia hết cho 3. Suy ra n(n + 1)(n + 2) chia hết cho 3.
Do đó n(n + 1)(n + 2) chia hết cho 3 với mọi số tự nhiên n (2).
Từ (1) và (2) suy ra n(n + 1)(n + 2) chia hết cho 2 và 3 với mọi số tự nhiên n hay tích của ba số tự nhiên liên tiếp chia hết cho 2, cho 3.
Suy ra phát biểu d) là đúng.
Vậy phát biểu sai là b) và c).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
Vì M chia cho 12 dư 10, nên ta viết M = 12.q + 10.
⇒ M = 2.6.q + 2.5 = 2.(6q +5) chia hết cho 2
Ta có: M = 3.4.q + 3.3 + 1 = 3.(4q + 3) + 1 ⇒ M chia 3 dư 1.
Do đó M không chia hết cho 3.
M = 4.3.q + 4.2 + 2 = 4 (3q + 2) + 2
⇒ M chia 4 dư 2.
Do đó M không chia hết cho 4.
Vậy M chia hết cho 2 nhưng không chia hết cho 3 và cho 4
Lời giải
Lời giải:
a) Ta có 15 = 5.3 nên 15 chia hết cho 3. Suy ra 15.16.17 chia hết cho 3.
Để P = 15.16.17 + a chia hết cho 3 thì a phải chia hết cho 3
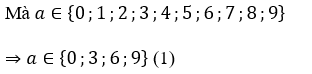
Ta lại có 15.16.17 = 3.5.2.8.17 = 3.10.8.17 chia hết cho 10.
Để P = 15.16.17 + a chia hết cho 10 thì a phải chia hết cho 10
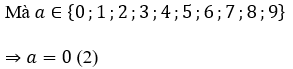
Từ (1) và (2) suy ra a = 0.
Vậy với a = 0 để P = 15.16.17 + a vừa chia hết cho 3 vừa chia hết cho 10.
b) Vì 125 có chữ số tận cùng là 5 nên 125 chia hết cho 5
Để 125 – a chia hết 5 thì a chia hết cho 5
Mà 90 < a < 100 nên a = 95
Vậy a = 95.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.