Viết kết quả phép chia dưới dạng a = b.q + r, với 0≤ r < b
a) 92 727:6 315;
b) 589 142:1 093;
c) 68 842: 6 329.
Quảng cáo
Trả lời:
Lời giải:
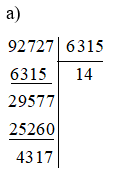
Suy ra 92 727:6 315 = 14 dư 4317 nên ta viết được: 92 727 = 6 315.14 + 4 317.
Vậy 92 727 = 6 315.14 + 4 317.
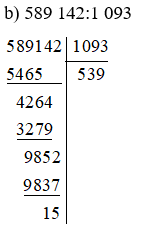
Suy ra 589 142:1 093 = 539 dư 15 nên ta viết được: 589 142 = 1 093.539 + 15.
Vậy 589 142 = 1 093.539 + 15.
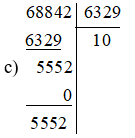
Suy ra 68 842: 6 329 = 10 dư 5552 nên ta viết được: 68 842 = 10.6 329 + 5552.
Vậy 68 842 = 10.6 329 + 5552.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
Vì M chia cho 12 dư 10, nên ta viết M = 12.q + 10.
⇒ M = 2.6.q + 2.5 = 2.(6q +5) chia hết cho 2
Ta có: M = 3.4.q + 3.3 + 1 = 3.(4q + 3) + 1 ⇒ M chia 3 dư 1.
Do đó M không chia hết cho 3.
M = 4.3.q + 4.2 + 2 = 4 (3q + 2) + 2
⇒ M chia 4 dư 2.
Do đó M không chia hết cho 4.
Vậy M chia hết cho 2 nhưng không chia hết cho 3 và cho 4
Lời giải
Lời giải:
a) Ta có 15 = 5.3 nên 15 chia hết cho 3. Suy ra 15.16.17 chia hết cho 3.
Để P = 15.16.17 + a chia hết cho 3 thì a phải chia hết cho 3
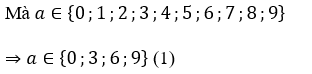
Ta lại có 15.16.17 = 3.5.2.8.17 = 3.10.8.17 chia hết cho 10.
Để P = 15.16.17 + a chia hết cho 10 thì a phải chia hết cho 10
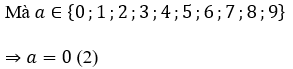
Từ (1) và (2) suy ra a = 0.
Vậy với a = 0 để P = 15.16.17 + a vừa chia hết cho 3 vừa chia hết cho 10.
b) Vì 125 có chữ số tận cùng là 5 nên 125 chia hết cho 5
Để 125 – a chia hết 5 thì a chia hết cho 5
Mà 90 < a < 100 nên a = 95
Vậy a = 95.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.