Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HE vuông góc với AB (E ∈ AB); kẻ HF vuông góc với AC (F ∈ AC).
a) Chứng minh: Tứ giác AEHF là hình chữ nhật.
b) Gọi P là điểm đối xứng của H qua AB. Tứ giác APEF là hình gì? Vì sao?
c) Đường thẳng đi qua C và song song với BP, cắt tia PA tại Q. Chứng minh: Q đối xứng với H qua F.
Câu hỏi trong đề: Đề thi Giữa kì 1 Toán 8 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
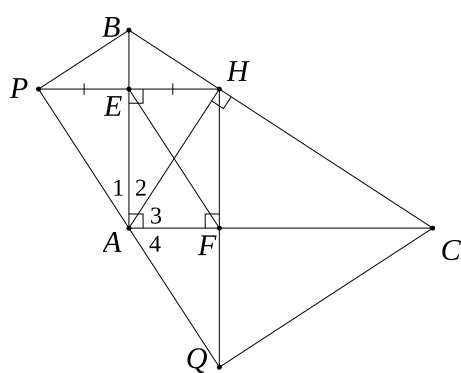
a) Tứ giác AEHF có:
\(\widehat A = 90^\circ \) (tam giác ABC vuông tại A)
HE ⊥ AB ⇒ \(\widehat {AEH} = 90^\circ \)
HF ⊥ AC ⇒ \(\widehat {AFH} = 90^\circ \)
⇒ Tứ giác AEHF là hình chữ nhật (tứ giác có 3 góc vuông)
b) Hình chữ nhật AEHF có:
EH // AF và EH = AF
Lại có: PE = EH (vì P là điểm đối xứng của H qua AB)
⇒ PE = AF (= EH)
Tứ giác APEF có:
EP // AF và PE = AF
⇒ Tứ giác APEF là hình bình hành. (Tứ giác có hai cạnh đối song song và bằng nhau)
c) Vì P đối xứng với H qua AB nên AB là đường trung trực của PH
⇒ AP = AH và BP = BH
Xét ΔAPB và ΔAHB có:
BP = PH
AP =AH
AB chung
⇒ ΔAPB = ΔAHB (c.c.c)
\( \Rightarrow \widehat {{A_1}} = \widehat {{A_2}}\) và \(\widehat {APB} = \widehat {AHB}\) (hai góc tương ứng)
Mà có \(\widehat {AHB} = 90^\circ \) nên \(\widehat {APH} = 90^\circ \)
Hay AP ⊥ PB
Ta có AP ⊥ PB và PB // CQ
⇒ AP ⊥ CQ hay AQ ⊥ CQ \( \Rightarrow \widehat {AQC} = 90^\circ \).
Ta có: \[\left\{ \begin{array}{l}\widehat {{A_4}} + \widehat {{A_1}} = 180^\circ - \widehat {BAC} = 90^\circ \\\widehat {{A_3}} + \widehat {{A_4}} = \widehat {BAC} = 90^\circ \end{array} \right.\] và \(\widehat {{A_1}} = \widehat {{A_2}}\) (cmt)
\( \Rightarrow \widehat {{A_3}} = \widehat {{A_4}}\)
Xét ΔAHC và ΔAQC có:
\(\widehat {{A_3}} = \widehat {{A_4}}\) (cmt)
AC chung
\(\widehat {AHC} = \widehat {AQC} = 90^\circ \)
⇒ ΔAHC = ΔAQC (cạnh huyền góc nhọn)
⇒ AH = AQ (hai cạnh tương ứng)
Xét ΔAHF và ΔAQF có:
\(\widehat {{A_3}} = \widehat {{A_4}}\) (cmt)
AF chung
AH = AQ (cmt)
⇒ ΔAHF = ΔAQF (c.g.c)
\( \Rightarrow \widehat {AFH} = \widehat {AFQ}\) (hai góc tương ứng)
Mà \(\widehat {AFH} = 90^\circ \) nên \(\widehat {AFQ} = 90^\circ \).
Ta có: \(\widehat {HFQ} = \widehat {AFH} + \widehat {AFQ} = 90^\circ + 90^\circ = 180^\circ \)
Hay H, F, Q thẳng hàng (1)
Vì ΔAHF = ΔAQF (cmt) nên HF = QF (2)
Từ (1) và (2) suy ra Q đối xứng với H qua F.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Vì 2n + 1 là số chính phương. Mà 2n + 1 là số lẻ (do 2n là số chẵn)
Suy ra 2n + 1 chia cho 8 dư 1.
Do đó n chia hết cho 4.
Suy ra n + 1 là số lẻ
Nên n + 1 chia cho 8 dư 1.
Vậy n chia hết cho 8. (1)
Mặt khác:
2n + 1 + n + 1 = 3n + 2 chia cho 3 dư 2.
Do đó (n + 1) + (2n + 1) chia cho 3 dư 2.
Mà n + 1 và 2n + 1 là các số chính phương lẻ
Suy ra n + 1 và 2n + 1 chia cho 3 dư 1.
Nên n chia hết cho 3. (2)
Từ (1) và (2) suy ra n đều chia hết cho cả 3 và 8.
Mà (3; 8) = 1 (3 và 8 là hai số nguyên tố cùng nhau)
Vậy n chia hết cho 24.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
a) x(5 – 6x) + (2x – 1)(3x + 4) = 6
5x – 6x2+ 6x2+ 5x – 4 – 6 = 0
10x – 10 = 0
x = 1
Vậy x = 1.
b) x2(x – 2021) – x + 2021 = 0
(x – 2021)(x2– 1) = 0
(x – 2021)(x – 1)(x + 1) = 0
\( \Rightarrow \left[ \begin{array}{l}x - 2021 = 0\\x - 1 = 0\\x + 1 = 0\end{array} \right.\)
\( \Rightarrow \left[ \begin{array}{l}x = 2021\\x = 1\\x = - 1\end{array} \right.\)
Vậy x = 1, x = – 1 và x = 2021.
c) 2x2– 3x – 5 = 0
2x2+ 2x – 5x – 5 = 0
2x(x + 1) – 5(x + 1) = 0
(x + 1)(2x – 5) = 0
\(\begin{array}{l} \Rightarrow \left[ \begin{array}{l}x + 1 = 0\\2x - 5 = 0\end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}x = - 1\\x = \frac{5}{2}\end{array} \right.\end{array}\)
Vậy x = – 1 và \(x = \frac{5}{2}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập