Một nguồn sáng đơn sắc [ lambda = 0,6 mu m ; ]chiếu vào một mặt phẳng chứa hai khe hở S1, S2hẹp, song song, cách nhau 1mm và cách đều nguồn sáng. Đặt một màn ảnh song song và cách mặt phẳng chứa hai...

Câu hỏi:

06/04/2022 1,941

Một nguồn sáng đơn sắc \[\lambda = 0,6\mu m\;\]chiếu vào một mặt phẳng chứa hai khe hở S₁, S₂hẹp, song song, cách nhau 1mm và cách đều nguồn sáng. Đặt một màn ảnh song song và cách mặt phẳng chứa hai khe 1m. Đặt trước khe S₁một bản thủy tinh 2 mặt phẳng song song có chiết suất n=1,5; độ dày \[e = 12\mu m\]. Vị trí hệ thống vân sẽ dịch chuyển trên màn thế nào?

A.Về phía S₁2mm

B.Về phía S₁6mm

C.Về phía S₂2mm

D.Về phía S₂6mm

Xem lời giải

Câu hỏi trong đề: ĐGNL ĐHQG Hà Nội - Khoa học tự nhiên - Giao thoa ánh sáng - Bài tập dịch nguồn, đặt bản mỏng !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

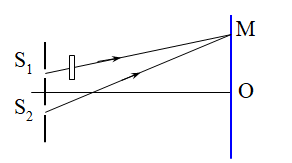
Khi đặt trước S₁một bản thủy tinh 2 mặt song song thì khi đó, hệ thống vân sẽ dịch chuyển một đoạn : \[{x_0} = \frac{{(n - 1)eD}}{a} = \frac{{(1,5 - 1){{.12.10}^{ - 6}}.1}}{{{{10}^{ - 3}}}} = {6.10^{ - 3}}m = 6mm\]về phía S₁

Đáp án cần chọn là: B

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một nguồn sáng đơn sắc \[\lambda = 0,6\mu m\]chiếu vào một mặt phẳng chứa hai khe S₁và S₂, hẹp, song song, cách nhau 1mm và cách đều nguồn sáng. Đặt một màn hứng ảnh song song và cách mặt phẳng chứa hai khe 1m. Ban đầu đặt sau khe S₂một bản thủy tinh song song có chiết suất n; độ dày e. Sau đó, không đặt bản thủy tinh mà đổ đầy vào khoảng giữa khe và màn một chất lỏng có chiết suất n’. Người ta thấy khoảng cách giữa hai vân sáng liên tiếp bằng 0,45mm. Tính chiết suất n’

A.1,6

B.1,5

C.1,4

D.1,33

Lời giải

Ta có, khoảng cách giữa 2 vân sáng liên tiếp là i = 0,45mm

\[i = \frac{{\frac{\lambda }{{n'}}D}}{a} \to n' = \frac{{\lambda D}}{{ia}} = \frac{{{{0,6.10}^{ - 6}}.1}}{{{{0,45.10}^{ - 3}}{{.10}^{ - 3}}}} = \frac{4}{3}\]

Đáp án cần chọn là: D

Câu 2

Trong thí nghiệm I-âng cho a = 2,5mm, D = 1,5m. Người ta đặt trước một trong hai khe sáng một bản mặt song song mỏng chiết suất n = 1,52. Khi đó, ta thấy hệ vân giao thoa trên màn bị dịch chuyển một đoạn 3mm. Bề dày e của bản mỏng là:

A.\[9,6\mu m\]

B.9,6nm

C.\[1,6\mu m\]

D.16nm

Lời giải

Giả sử đặt trước S₁bản mặt song song, ta có:

Khi đặt trước S₁một bản thủy tinh 2 mặt song song thì khi đó, hệ thống vân sẽ dịch chuyển một đoạn : \[{x_0} = \frac{{(n - 1)eD}}{a}\]về phía S₁

Theo đầu bài, ta có:

\[{x_0} = 3mm = \frac{{(n - 1)eD}}{a} \to e = \frac{{a{x_0}}}{{(n - 1)D}} = \frac{{{{2,5.10}^{ - 3}}{{.3.10}^{ - 3}}}}{{(1,52 - 1).1,5}} \approx {9,62.10^{ - 6}}m = 9,62\mu m\]Đáp án cần chọn là: A

Câu 3