ĐGNL ĐHQG Hà Nội - Khoa học tự nhiên - Giao thoa ánh sáng - Bài tập dịch nguồn, đặt bản mỏng
60 người thi tuần này 4.6 2.6 K lượt thi 8 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 45)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 44)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 43)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 42)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 41)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 40)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 39)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 38)
Danh sách câu hỏi:
Câu 1
A.\[0,75\mu m\]
B. \[0,67\mu m\]
C. 750pm
D. 670pm
Lời giải
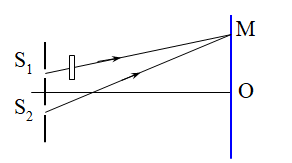
Ta có: Khi đặt trước S1một bản thủy tinh 2 mặt song song thì khi đó, hệ thống vân sẽ dịch chuyển một đoạn : \[{x_0} = \frac{{(n - 1)eD}}{a}\]về phía S1
Theo đầu bài, ta có: khoảng dịch chuyển đó bằng khoảng cách giữa 9 vân sáng liên tiếp
Ta có, khoảng cách giữa 9 vân sáng liên tiếp là: 8i
\[\begin{array}{*{20}{l}}{ \to {x_0} = 8i \leftrightarrow \frac{{(n - 1)eD}}{a} = 8\frac{{\lambda D}}{a}}\\{ \to \lambda = \frac{{(n - 1)e}}{8} = \frac{{(1,5 - 1){{.12.10}^{ - 6}}}}{8} = {{0,75.10}^{ - 6}}m = 0,75\mu m}\end{array}\]
Đáp án cần chọn là: A
Câu 2
A.\[11,25\mu m\]
B. \[122,5\mu m\]
C. \[22,5\mu m\]
D. \[45\mu m\]
Lời giải
Giả sử đặt trước S1mảnh mica phẳng, ta có:

Ta có: Khi đặt trước S1bản mica thì khi đó, hệ thống vân sẽ dịch chuyển một đoạn :
\[{x_0} = \frac{{(n - 1)eD}}{a}\]về phía S1
Theo đầu bài ta có: đoạn dịch chuyển này bằng 30i
\[\begin{array}{*{20}{l}}{{x_0} = 30i \leftrightarrow \frac{{(n - 1)eD}}{a} = 30i = \frac{{30\lambda D}}{a}}\\{ \to e = \frac{{30\lambda }}{{(n - 1)}} = \frac{{{{30.450.10}^{ - 9}}}}{{(1,6 - 1)}} = {{2,25.10}^{ - 5}}m = 22,5\mu m}\end{array}\]
Đáp án cần chọn là: C
Lời giải
Giả sử đặt trước S1bản mặt song song, ta có:

Khi đặt trước S1một bản thủy tinh 2 mặt song song thì khi đó, hệ thống vân sẽ dịch chuyển một đoạn : \[{x_0} = \frac{{(n - 1)eD}}{a}\]về phía S1
Theo đầu bài, ta có:
\[{x_0} = 3mm = \frac{{(n - 1)eD}}{a} \to e = \frac{{a{x_0}}}{{(n - 1)D}} = \frac{{{{2,5.10}^{ - 3}}{{.3.10}^{ - 3}}}}{{(1,52 - 1).1,5}} \approx {9,62.10^{ - 6}}m = 9,62\mu m\]Đáp án cần chọn là: A
Câu 4
A.\[0,40\mu m\]
B. \[0,58\mu m\]
C. \[0,60\mu m\]
D. \[0,75\mu m\]
Lời giải
Gọi i và i’ là khoảng vân ban đầu và sau khi dời màn
D, D’ là khoảng cách giữa hai khe và màn lúc ban đầu và sau khi dời màn
Ta có:
+ Ban đầu:\[i = \frac{{\lambda D}}{a}\]
+ Khi dời màn :\[i' = \frac{{\lambda D'}}{a}\]
Mặt khác, theo đầu bài: Khoảng vân tăng thêm 0,3mm khi khoảng cách giữa màn và hai khe thay đổi 0,5m
\[D' >D \to D' = D + 0,5\]
\[\begin{array}{*{20}{l}}{i' - i = 0,3mm = {\rm{\Delta }}i \leftrightarrow \frac{{\lambda D'}}{a} - \frac{{\lambda D}}{a} = {\rm{\Delta }}i}\\{ \leftrightarrow \frac{\lambda }{a}(D' - D) = {\rm{\Delta }}i \to \lambda = \frac{{{\rm{\Delta }}i.a}}{{D' - D}} = \frac{{{{0,3.10}^{ - 3}}{{.10}^{ - 3}}}}{{0,5}} = {{0,6.10}^{ - 6}}m}\end{array}\]
Đáp án cần chọn là: C
Câu 5
A.Về phía S1một đoạn \[{x_0} = \frac{{(1 - n)eD}}{a}\]
B.Về phía S2một đoạn \[{x_0} = \frac{{(1 - n)eD}}{a}\]
C.Về phía S1một đoạn \[{x_0} = \frac{{(1 - n)eD}}{a}\]
D.Về phía S2một đoạn \[{x_0} = \frac{{(1 - n)eD}}{a}\]
Lời giải
Khi đặt trước S1một bản thủy tinh 2 mặt song song thì khi đó, hệ thống vân sẽ dịch chuyển một đoạn \[{x_o}\, = \,\frac{{(n\, - \,1)eD}}{a}\]về phía S1
Đáp án cần chọn là: C
Câu 6
A.Về phía S12mm
B.Về phía S16mm
C.Về phía S22mm
D.Về phía S26mm
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.