Cho hàm số có đồ thị như hình vẽ bên dưới. Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc khoảng để hàm số đồng biến trên nửa khoảng .
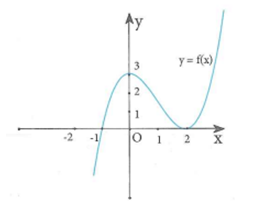
Cho hàm số có đồ thị như hình vẽ bên dưới. Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc khoảng để hàm số đồng biến trên nửa khoảng .
A. 2019
B. 2020
C. 4038
D. 4040
Quảng cáo
Trả lời:
Đáp án A
Ta có
Hàm số liên tục trên nửa khoảng
Hàm số đồng biến trên khi và chỉ khi
(1)
Do nên (2)
Dựa vào đồ thị ta có
Xét hàm trên có nên đồng biến trên đồng thời liên tục trên
Suy ra và .
Do đó, không có giá trị m thỏa mãn (4)
Vậy có tất cả 2019 giá trị nguyên của tham số m.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án D
Số các số tự nhiên có 4 chữ số đôi một khác nhau được lập từ 7 chữ số 1, 2, 3, 4, 5, 6, 7 là số.
Lời giải
Đáp án A
có VTPT , có VTPT , có VTPT .
Chọn thuộc giao tuyến của hai mặt phẳng ,
Gọi d là giao tuyến của hai mặt phẳng và khi đó d đi qua điểm và có VTCP
đi qua giao tuyến của hai mặt phẳng , và vuông góc với
Mặt phẳng đi qua và nhận làm vectơ pháp tuyến có phương trình
Câu 3
A. Đồ thị của hàm số và đối xứng với nhau qua đường thẳng
B. Đồ thị của hai hàm số và đối xứng với nhau qua đuường thẳng
C. Đồ thị của hai hàm số và đối xứng với nhau qua trục hoành
D. Đồ thị của hai hàm số và đối xứng với nhau qua trục tung
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.