Câu hỏi:

05/05/2022 9,729

Trong ao có 10 lá sen thẳng hàng, nằm sát mặt nước. Một con ếch đứng ở chiếc lá sen đầu tiên và nó định nhảy đến chiếc lá cuối cùng. Mỗi lần nó có thể nhảy tiến tới tích 1 hoặc 2 bước (tức là không quay lại). Hòi nó có bao nhiêu cách nhảy để đến đích?

A. 47

B. 51

C. 54

D. 55

Xem lời giải

Câu hỏi trong đề: Đề thi Đánh giá tư duy Đọc hiểu, Toán học - ĐH Bách khoa năm 2023 - 2024 có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Chọn D

Phương pháp giải:

Chia trường hợp theo số lần nhảy 2 bước của con ếch

Mỗi trường hợp sẽ có số cách nhảy tương ứng

Dùng quy tắc cộng

Giải chi tiết:

Nếu con ếch nhảy 4 lần 2 bước và 1 lần 1 bước: Số cách nhảy là số cách chọn vị trí của 1 bước nhảy trong 5 vị trí, là $C_{5}^{1}$ cách

Nếu con ếch nhảy 3 lần 2 bước và 3 lần 1 bước: Số cách nhảy là số cách chọn vị trí của 3 bước nhảy trong 6 vị trí, là $C_{6}^{3}$ cách

Tương tự với các trường hợp con ếch nhảy 2;1;0 lần 2 bước.

Tổng số cách nhảy theo quy tắc cộng là $C_{5}^{1} + C_{6}^{3} + C_{7}^{5} + C_{8}^{7} + C_{9}^{9} = 55$ cách

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong không gian Oxyz cho mặt cầu $(S) : {(x - 1)}^{2} + y^{2} + {(z - 2)}^{2} = 10$ và hai điểm A(1;2;-4); B(1;2;14). Điểm M(a;b;c) là điểm nằm trên mặt cầu (S) sao cho P = MA + 2MB đạt GTNN. Khi đó a+b+c bằng:

A. $\frac{7}{41}$

B. $\frac{23}{41}$

C. 4

D. 7

Lời giải

Chọn D

Phương pháp giải:

Gọi điểm C thỏa mãn MA = 2MC

GTNN của MA + 2MB là BC

Tìm giao của BC với mặt cầu, chính là điểm M cần tìm

Giải chi tiết:

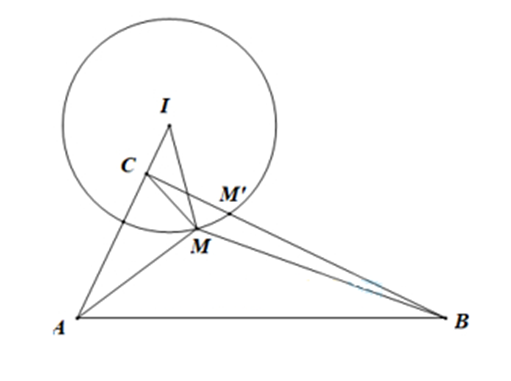
Trong không gian Õyz cho mặt cầu (S): (x-1)^2+y^2+(z-2)^2=10 và hai điểm A(1;2;-4) ;B(1;2;14) . Điểm M(a.b.c) là điểm nằm trên (ảnh 1)

Mặt cầu (S) có tâm $I (1; 0; 2)$ và bán kính $R = \sqrt{10}$ . Có

$\vec{IA} = (0; 2; - 6); IA = \sqrt{2^{2} + 6^{2}} = 2 \sqrt{10} = 2 R$

Gọi C là điểm thỏa mãn $\vec{I C} = \frac{1}{4} \vec{I A} = (0; \frac{1}{2}; - \frac{3}{2}) \Rightarrow C (1; \frac{1}{2}; \frac{1}{2})$

Có ${IM}^{2} = IC$ . IA $\Rightarrow Δ IMC ~ Δ IAM$ (c. g.c)

\Rightarrow \frac{MA}{MC} = \frac{IA}{IM} = 2 \Rightarrow MA = 2 MC \Rightarrow MA + 2 MB = 2 (MB + MC) \geq BC

Đẳng thức xảy ra khi M trùng M ' là giao của đoạn BC với (S)

M’ thuộc đoạn BC $\Leftrightarrow \vec{C M'} = k \vec{C B} = (0; \frac{3}{2} k; \frac{27}{2} k) (k > 0)$

$\Leftrightarrow M^{'} (1; \frac{1}{2} + \frac{3}{2} k; \frac{1}{2} + \frac{27}{2} k)$ . Ta có

M^{'} \in (S) \Leftrightarrow {IM}^{'} = \sqrt{10} \Leftrightarrow 0 + {(\frac{1}{2} + \frac{3}{2} k)}^{2} + {(\frac{27}{2} k - \frac{3}{2})}^{2} = 10

\Leftrightarrow k = \frac{1}{3} \Rightarrow M^{'} (1; 1; 5) .

Vậy $a + b + c = 7$ .

Câu 2

Cho hàm số bậc ba $y = f (x)$ có đồ thị như hình vẽ. Tổng số đường tiệm cận của đồ thị hàm số $y = \frac{(x^{2} - 2 x) \sqrt{2 - x}}{(x - 3) [f^{2} (x) + 3 f (x)]}$ là?

A. 3

B. 4

C. 5

D. 6

Lời giải

Chọn C

Phương pháp giải:

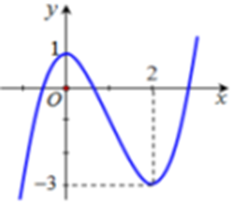
Cách tìm số các tiệm cận:

+ Tiệm cận ngang: Cho x tiến tới dương vô cùng và âm vô cùng

+ Tiệm cận đứng: Tìm các nghiệm của mẫu thức, loại đi các nghiệm không phù hợp.

Giải chi tiết:

ĐK: {x≤2f2(x)+3f(x)≠0{x≤2f2(x)+3f(x)≠0

+ Tiệm cận ngang:

Vì hàm số y là hàm số phân thức, có bậc của tử nhỏ hơn bậc của mẫu nên $\lim_{x \to - \infty} y = 0$ .

⇒ Đồ thị có 1 TCN y=0.

+ Tiệm cận đứng:

Ta có $(x - 3) [f^{2} (x) + 3 f (x)] = 0$

$[\begin{array}{l} x = 3 (L) \\ f (x) = 0 \\ f (x) = - 3 \end{array} \Leftrightarrow [\begin{array}{l} x = x_{1} > 2 \\ x = z_{2} \in (- 1; 0) \\ x = x_{3} \in (0; 1) \\ x = 2 \end{array}$

Vì x=2 là nghiệm kép của mẫu, nên mẫu sẽ có nhân tử ${(x - 2)}^{2}$ . Do đó x=2 là một TCĐ.

Suy ra đồ thị hàm số có 4 TCĐ.

Vậy tổng số tiệm cận là 5.

Câu 3

1. Tìm tất cả các giá trị của m để hàm số $y = \frac{1}{3} m x^{3} - (m - 1) x^{2} + 3 (m - 2) x + 2022$ đồng biến trên $[2; + \infty)$

2. Cho dãy số (u_n) có số hạng tổng quát $u_{1} = 1 - \frac{1}{{(n + 1)}^{2}}, \forall n \in ℕ *$ . Tính $l i m (u_{1} u_{2} ... u_{n})$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Có 6 học sinh gồm 1 học sinh lớp 10, 2 học sinh lớp 11 và 3 học sinh lớp 12 được xếp ngẫu nhiên thành một hàng dọc. Xác suất học sinh lớp 10 đứng xen kẽ giữa 2 học sinh lớp 12 là:

A. $\frac{1}{10}$

B. $\frac{3}{5}$

C. $\frac{1}{5}$

D. $\frac{3}{10}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Sự phân rã của một đồng vị phóng xạ được biểu diễn theo công thức $m (t) = m_{0} {(\frac{1}{2})}^{\frac{t}{r}}$ trong đó $m_{0}$ là khối lượng ban đầu của đồng vị phóng xạ (tại thời điểm $t = 0$ ); là chu kỳ bán rã của đồng vị đó. Biết rằng chu kỳ bán rã của đồng vị cacbon 14 (¹⁴C) là khoảng 5730 năm, hỏi một mẫu đồ cổ có độ tuổi là bao nhiêu năm biết rằng trong mẫu đồ cổ này chứa đồng vị cacbon 14 và đồng vị này đã mất khoảng 25% khối lượng ban đầu của nó?

A. 2300 năm

B. 2378 năm

C. 2387 năm

D. 2400 năm

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Tứ điện đều ABCD có cạnh a. Mặt cầu (S) tiếp xúc với AB, AC, AD lần lượt tại B, C, D giới hạn nên một hình cầu có thể tích là:

A. $\frac{π a^{3} \sqrt{3}}{2}$

B. $\frac{4 π a^{3}}{81}$

C. $\frac{π a^{3} \sqrt{2}}{3}$

D. $\frac{8 π a^{3}}{27}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Trong không gian Oxyz cho mặt cầu $(S) : {(x - 1)}^{2} + y^{2} + {(z - 2)}^{2} = 10$ và hai điểm A(1;2;-4); B(1;2;14). Điểm M(a;b;c) là điểm nằm trên mặt cầu (S) sao cho P = MA + 2MB đạt GTNN. Khi đó a+b+c bằng:

Cho hàm số bậc ba $y = f (x)$ có đồ thị như hình vẽ. Tổng số đường tiệm cận của đồ thị hàm số $y = \frac{(x^{2} - 2 x) \sqrt{2 - x}}{(x - 3) [f^{2} (x) + 3 f (x)]}$ là?