Trong không gian với hệ trục tọa độ vuông góc Oxyz, cho mặt phẳng , mặt cầu . Gọi là đường thẳng nằm trong mặt phẳng P, đi qua và cắt (S) tại 2 điểm M, N. Độ dài đoạn thẳng MN nhỏ nhất là
Quảng cáo
Trả lời:
Phương pháp giải:
Tìm tâm I, bán kính R của mặt cầu (S) và vtpt của mặt phẳng (P)
Giải chi tiết:
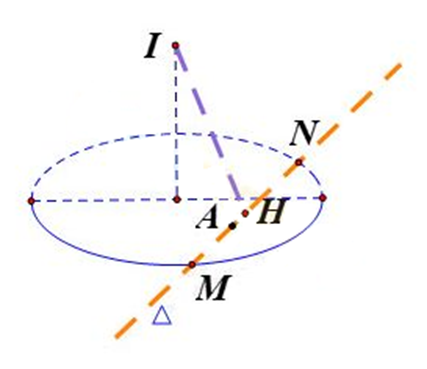
Mặt cầu (S) có tâm I(5;2;3), bán kính .
Mặt phẳng (P) có .
Ta có: => Mặt phẳng (P) cắt mặt cầu (S).
⇒ Điểm A nằm trong mặt cầu.
Gọi H là trung điểm của MN. Khi đó IH vuông góc với MN
Do đó MN min ⇔ IH max
Vì tam giác IAH vuông tại H
=> MN min .
Chọn B
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp giải:
Bước 1: Kẻ AH vuông góc với SB. Chứng minh AH⊥(SBC)
Bước 2: Tính AH
Giải chi tiết:
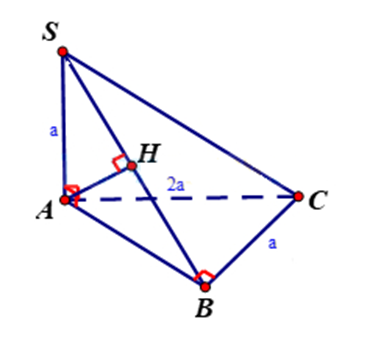
Bước 1: Kẻ AH vuông góc với SB. Chứng minh
Kẻ AH vuông góc với SB.
Ta có:
Lại có
Bước 2: Tính AH
Xét tam giác vuông ABC có:
Xét tam giác vuông SAB có:
Chọn D
Câu 2
Lời giải
Chọn A
Phương pháp giải:
Bước 1: Gọi số cần tìm là
Tách các bộ số chia hết cho 3, chia 3 dư 1 và chia 3 dư 2.
Bước 2: Xét các trường hợp bộ số chia hết cho 3
+) a, b, c đều chia hết cho 3
+)
+) .
+) Trong 3 số a, b, c có 1 số chia hết cho 3, 1 số chia 3 dư 1, 1 số chia 3 dư 2.
Giải chi tiết:
Bước 1:
Gọi số cần tìm là
Từ các số bài cho ta chia thành 3 bộ số:
+ Bộ số chia hết cho 3 là: 3; 6; 9
+ Bộ số chia cho 3 dư 1 là: 1; 4; 7
+ Bộ số chia cho 3 dư 2 là: 2; 5; 8
Bước 2:
Xét các trường hợp sau:
+) a, b, c đều chia hết cho 3 Có 3! số.
+) => Có 3! số.
+) ⇒ Có 3!số.
+) Trong 3 số a, b, c có 1 số chia hết cho 3, 1 số chia 3 dư 1, 1 số chia 3 dư 2
Vậy có 3.3!+162=180 số thỏa mãn đề bài.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.