Trong hình vẽ, xe A kéo xe B bằng một sợi dây dài 39m qua một ròng rọc ở độ cao 12m. Xe A xuất phát từ N và chạy với vận tốc không đổi 2 m/s theo chiều mũi tên.
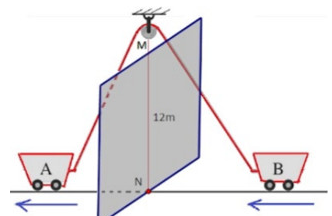
a) Đặt và , (đơn vị mét). Tìm một hệ thức liên hệ giữa x và y .
b) Tính vận tốc của xe B khi xe A cách N một đoạn 5m.
Trong hình vẽ, xe A kéo xe B bằng một sợi dây dài 39m qua một ròng rọc ở độ cao 12m. Xe A xuất phát từ N và chạy với vận tốc không đổi 2 m/s theo chiều mũi tên.

a) Đặt và , (đơn vị mét). Tìm một hệ thức liên hệ giữa x và y .
b) Tính vận tốc của xe B khi xe A cách N một đoạn 5m.
Quảng cáo
Trả lời:
a) Phương pháp giải:
Coi M, A, B là một tam giác và N thuộc cạnh AB
Bước 1: Xác định AM+BMAM+BM, MN
Bước 2: Tìm mối liên hệ giữa x và y.
Giải chi tiết:
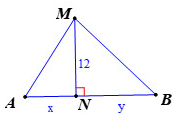
Bước 1: Xác định AM + BM, MN
Coi M,A,B là một tam giác và N thuộc cạnh AB
Sợi dây dài .
Có MN=12.
Bước 2: Tìm mối liên hệ giữa ![]() và y.
và y.
Theo định lý py-ta-go ta được:
Vậy hệ thức cần tìm là
b) Phương pháp giải:
Gọi t là thời gian xe A di chuyển.
Bước 1: Tìm mối quan hệ giữa x và t
Bước 2: Tìm mối quan hệ giữa y và t
Bước 3: Tính quãng đường tại t=2,5(s).
Giải chi tiết:
Bước 1: Tìm mối quan hệ giữa x và t
Khi A sang trái thì x tăng dần và y giảm dần
Tạo mối quan hệ giữa y và t
Vì xe A chuyển động đều với vận tốc là 2m/s nên mối quan hệ giữa x và t là:
Bước 2: Tìm mối quan hệ giữa y và t
Mà ta có nên:
Quãng đường A đi được là 5m nên ta có t=2,5(s)
Bước 3: Tính quãng đường tại t=2,5(s)
Vận tốc tại thời điểm t=2,5(s) của B là y′(2,5). Khi đó
Vậy .
Vận tốc tức thời của xe B tại thời điểm xe A cách N 5m là -0,867(m/s).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp giải:
Bước 1: Kẻ AH vuông góc với SB. Chứng minh AH⊥(SBC)
Bước 2: Tính AH
Giải chi tiết:
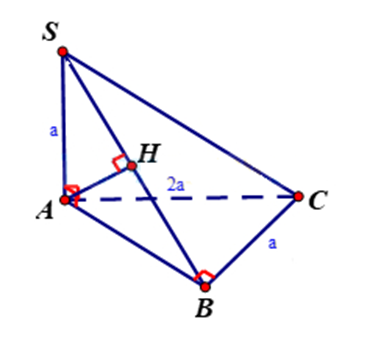
Bước 1: Kẻ AH vuông góc với SB. Chứng minh
Kẻ AH vuông góc với SB.
Ta có:
Lại có
Bước 2: Tính AH
Xét tam giác vuông ABC có:
Xét tam giác vuông SAB có:
Chọn D
Câu 2
Lời giải
Chọn A
Phương pháp giải:
Bước 1: Gọi số cần tìm là
Tách các bộ số chia hết cho 3, chia 3 dư 1 và chia 3 dư 2.
Bước 2: Xét các trường hợp bộ số chia hết cho 3
+) a, b, c đều chia hết cho 3
+)
+) .
+) Trong 3 số a, b, c có 1 số chia hết cho 3, 1 số chia 3 dư 1, 1 số chia 3 dư 2.
Giải chi tiết:
Bước 1:
Gọi số cần tìm là
Từ các số bài cho ta chia thành 3 bộ số:
+ Bộ số chia hết cho 3 là: 3; 6; 9
+ Bộ số chia cho 3 dư 1 là: 1; 4; 7
+ Bộ số chia cho 3 dư 2 là: 2; 5; 8
Bước 2:
Xét các trường hợp sau:
+) a, b, c đều chia hết cho 3 Có 3! số.
+) => Có 3! số.
+) ⇒ Có 3!số.
+) Trong 3 số a, b, c có 1 số chia hết cho 3, 1 số chia 3 dư 1, 1 số chia 3 dư 2
Vậy có 3.3!+162=180 số thỏa mãn đề bài.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.