Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
“Tràng giang có chất Đường thi hơn những bài thơ Đường trung đại. Chính Huy Cận cũng thừa nhận ông đã lấy cảm hứng từ ý thơ của Đỗ Phủ, Thôi Hiệu đời Đường, của Chinh phụ ngâm để cho bài thơ đạt đến tác phong cổ điển.”
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
“Tràng giang có chất Đường thi hơn những bài thơ Đường trung đại. Chính Huy Cận cũng thừa nhận ông đã lấy cảm hứng từ ý thơ của Đỗ Phủ, Thôi Hiệu đời Đường, của Chinh phụ ngâm để cho bài thơ đạt đến tác phong cổ điển.”
A. thừa nhận
Quảng cáo
Trả lời:
Phương pháp giải:
Căn cứ vào nghĩa của từ
Giải chi tiết:
Tác phong: Có nghĩa là cách thức làm việc, sinh hoạt hằng ngày của mỗi người. Sử dụng ở đây không phù hợp
=> Chữa lại: phong vị (đặc tính gây hứng thú đặc sắc)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. Được các nước Đồng minh thiết lập quan hệ ngoại giao.
Lời giải
Phương pháp giải:
Suy luận, loại trừ phương án.
Giải chi tiết:
A loại vì các nước Đồng minh không thiết lập quan hệ ngoại giao với nước Việt Nam Dân chủ Cộng hòa trong những năm 1945 – 1946.
B chọn vì nhân dân ta đã giành được quyền làm chủ, bước đầu được hưởng quyền lợi do chính quyền cách mạng đưa đến nên rất phấn khởi, gắn bó với chế độ và quyết tâm bảo vệ chế độ dân chủ cộng hòa.
C loại vì Liên Xô công nhận và đặt quan hệ ngoại giao với ta năm 1950.
D loại vì Việt Nam nhận được sự ủng hộ và giúp đỡ của các nước xã hội chủ nghĩa từ năm 1950.
Lời giải
Phương pháp giải:
- Gọi \(E\) là trung điểm của \(AB\).
- Đánh giá GTNN của tích \(\overrightarrow {MA} .\overrightarrow {MB} \) đạt được dựa vào điểm \(E\).
Giải chi tiết:
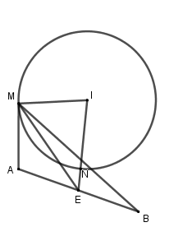
Mặt cầu \(\left( S \right)\) có tâm \(I\left( { - 1;2;1} \right)\) và bán kính \(R = \frac{{\sqrt 6 }}{2}\).
Gọi \(E\) là trung điểm của \(AB\)\( \Rightarrow E\left( {1; - 2; - 1} \right)\) và \(AB = 6\sqrt 2 \).
Ta có:
Suy ra \(\overrightarrow {MA} .\overrightarrow {MB} \) đạt GTNN khi \(ME\) đạt GTNN.
Lại có: \(ME + MI \ge IE \Rightarrow ME + MI \ge IN + NE \Rightarrow ME \ge NE\)
\( \Rightarrow ME\) đạt GTNN khi \(M \equiv N\) với \(N = IE \cap \left( S \right)\)
Đường thẳng \(IE\) đi qua \(I\left( { - 1;2;1} \right)\) và nhận làm VTCP nên
\(N = IE \cap \left( S \right)\) nên \({\left( { - 1 + t} \right)^2} + {\left( {2 - 2t} \right)^2} + {\left( {1 - t} \right)^2} + 2\left( { - 1 + t} \right) - 4\left( {2 - 2t} \right) - 2\left( {1 - t} \right) + \frac{9}{2} = 0\)
\( \Leftrightarrow 6{\left( {t - 1} \right)^2} + 12\left( {t - 1} \right) + \frac{9}{2} = 0\)
\( \Rightarrow \left[ {\begin{array}{*{20}{l}}{N\left( { - \frac{1}{2};1;\frac{1}{2}} \right) \Rightarrow NE = \frac{{3\sqrt 6 }}{2}}\\{N\left( { - \frac{3}{2};3;\frac{3}{2}} \right) \Rightarrow NE = \frac{{5\sqrt 6 }}{2}}\end{array}} \right.\)
\(M{E_{\min }} = \frac{{3\sqrt 6 }}{2}\) khi
Câu 3
A. \[M(1;3;0)\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. chủ động đánh địch và mở hàng loạt các cuộc tiến công địch ở đồng bằng sông Cửu Long.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. máy hạ áp, k = 0,5.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.