Câu hỏi:

21/05/2022 3,082

Muối Mohr là một muối kép ngậm 6 phân tử nước được tạo thành từ hỗn hợp đồng mol sắt(II) sunfat ngậm 7 phân tử nước và amoni sunfat khan.

FeSO₄.7H₂O + (NH₄)₂SO₄ → FeSO₄.(NH₄)₂SO₄.6H₂O + H₂O

Cho độ tan của muối Mohr ở 20⁰C là 26,9 g/100 g H₂O và ở 80⁰C là 73,0 g/100g H₂O. Tính khối lượng của muối sắt(II) sunfat ngậm 7 nước cần thiết để tạo thành dung dịch muối Mohr bão hòa 80⁰C, sau khi làm nguội dung dịch này xuống 20⁰C để thu được 100 gam muối Mohr tinh thể và dung dịch bão hòa. Giả thiết trong quá trình kết tinh nước bay hơi không đáng kể.

A. 213,2 gam.

B. 132,1 gam.

C. 321,1 gam.

D. 112,3 gam.

Xem lời giải

Câu hỏi trong đề: Top 10 đề thi Đánh giá năng lực trường ĐHQG Hà Nội năm 2023 - 2024 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Phương pháp giải:

Độ tan của một chất trong nước là số gam chất đó hòa tan trong 100 gam nước để tạo thành dung dịch bão hòa ở một nhiệt độ xác định.

Giải chi tiết:

Đặt x là số mol muối Mohr có trong dung dịch bão hòa ở 80⁰C

→ m_{muối Mohr} = m_{FeSO4.(NH4)2SO4.6H2O} = 392x (g)

Ở 80⁰C cứ 73 gam muối Mohr tan được trong 100 gam nước để tạo thành 173 gam dd bão hòa

→ 392x gam muối Mohr................................................................928,9863x gam dd bão hòa

Khi làm nguội dung dịch từ 80⁰C xuống 20⁰C thì tách ra 100 gam muối Mohr tinh thể

→ Khối lượng muối Mohr còn lại trong dung dịch = 392x - 100 (g)

→ Khối lượng dung dịch còn lại = 928,9863x - 100 (g)

Ta có: ở 20⁰C cứ 26,9 gam muối Mohr tan trong 100 gam nước tạo thành 126,9 gam dd bão hòa

Vậy cứ 392x - 100 gam muối Mohr ..........................................928,9863x - 100 gam dd bão hòa

→ 26,9.(928,9863x - 100) = 126,9.(392x - 100)

→ x = 0,404 (mol)

→ m_muối Mohr = 0,404 × 392 = 158,368 (g)

→ ${m_{F{\rm{eS}}{{\rm{O}}_4}.7{H_2}O}} = 0,404 \times 278 = 112,312\left( g \right)$

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong những năm 1945-1946, nước Việt Nam Dân chủ Cộng hòa có thuận lợi nào sau đây?

A. Được các nước Đồng minh thiết lập quan hệ ngoại giao.

B. Nhân dân quyết tâm bảo vệ chế độ dân chủ cộng hòa.

C. Được Liên Xô công nhận và đặt quan hệ ngoại giao.

D. Có sự ủng hộ và giúp đỡ của các nước xã hội chủ nghĩa.

Lời giải

Phương pháp giải:

Suy luận, loại trừ phương án.

Giải chi tiết:

A loại vì các nước Đồng minh không thiết lập quan hệ ngoại giao với nước Việt Nam Dân chủ Cộng hòa trong những năm 1945 – 1946.

B chọn vì nhân dân ta đã giành được quyền làm chủ, bước đầu được hưởng quyền lợi do chính quyền cách mạng đưa đến nên rất phấn khởi, gắn bó với chế độ và quyết tâm bảo vệ chế độ dân chủ cộng hòa.

C loại vì Liên Xô công nhận và đặt quan hệ ngoại giao với ta năm 1950.

D loại vì Việt Nam nhận được sự ủng hộ và giúp đỡ của các nước xã hội chủ nghĩa từ năm 1950.

Câu 2

Trong không gian Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} + 2 x - 4 y - 2 z + \frac{9}{2} = 0$ và hai điểm $A(0;2;0)$ $,B(2; - 6; - 2)$. Điểm $M\left( {a;b;c} \right)$ thuộc $\left( S \right)$ thỏa mãn tích $\vec{M A} \cdot \vec{M B}$ có giá trị nhỏ nhất. Tổng $a + b + c$ bằng

A. $ - 1$

B. 1

C. 3

D. 2

Lời giải

Phương pháp giải:

- Gọi $E$ là trung điểm của $AB$.

- Đánh giá GTNN của tích $\overrightarrow {MA} .\overrightarrow {MB} $ đạt được dựa vào điểm $E$.

Giải chi tiết:

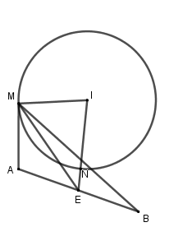
Trong không gian Oxyz, cho mặt cầu (ảnh 1)

Mặt cầu $\left( S \right)$ có tâm $I\left( { - 1;2;1} \right)$ và bán kính $R = \frac{{\sqrt 6 }}{2}$.

Gọi $E$ là trung điểm của $AB$$ \Rightarrow E\left( {1; - 2; - 1} \right)$ và $AB = 6\sqrt 2 $.

Ta có: $\vec{M A} . \vec{M B} = (\vec{M E} + \vec{E A}) (\vec{M E} + \vec{E B})$

$= M E^{2} + \vec{M E} . (\vec{E A} + \vec{E B}) + \vec{E A} . \vec{E B}$

$= M E^{2} + \vec{M E} . \vec{0} - \vec{E B} . \vec{E B} = M E^{2} - \frac{1}{4} A B^{2}$

Suy ra $\overrightarrow {MA} .\overrightarrow {MB} $ đạt GTNN khi $ME$ đạt GTNN.

Lại có: $ME + MI \ge IE \Rightarrow ME + MI \ge IN + NE \Rightarrow ME \ge NE$

$ \Rightarrow ME$ đạt GTNN khi $M \equiv N$ với $N = IE \cap \left( S \right)$

Đường thẳng $IE$ đi qua $I\left( { - 1;2;1} \right)$ và nhận $\vec{I E} = (2; - 4; - 2)$ làm VTCP nên $I E : {\begin{matrix} x = - 1 + t \\ y = 2 - 2 t \\ z = 1 - t \end{matrix}$

$N = IE \cap \left( S \right)$ nên ${\left( { - 1 + t} \right)^2} + {\left( {2 - 2t} \right)^2} + {\left( {1 - t} \right)^2} + 2\left( { - 1 + t} \right) - 4\left( {2 - 2t} \right) - 2\left( {1 - t} \right) + \frac{9}{2} = 0$

$ \Leftrightarrow 6{\left( {t - 1} \right)^2} + 12\left( {t - 1} \right) + \frac{9}{2} = 0$

$\Leftrightarrow [\begin{matrix} t - 1 = - \frac{1}{2} \\ t - 1 = - \frac{3}{2} \end{matrix} \Leftrightarrow [\begin{matrix} t = \frac{1}{2} \\ t = - \frac{1}{2} \end{matrix}$ $ \Rightarrow \left[ {\begin{array}{*{20}{l}}{N\left( { - \frac{1}{2};1;\frac{1}{2}} \right) \Rightarrow NE = \frac{{3\sqrt 6 }}{2}}\\{N\left( { - \frac{3}{2};3;\frac{3}{2}} \right) \Rightarrow NE = \frac{{5\sqrt 6 }}{2}}\end{array}} \right.$

$M{E_{\min }} = \frac{{3\sqrt 6 }}{2}$ khi $M \equiv N (- \frac{1}{2}; 1; \frac{1}{2}) \Rightarrow a + b + c = - \frac{1}{2} + 1 + \frac{1}{2} = 1 .$

Câu 3

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng $\left( P \right):x + 2y - 2z + 3 = 0$ và $\left( Q \right):x + 2y - 2z - 1 = 0$. Khoảng cách giữa hai mặt phẳng (P) và (Q) là:

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Dựa vào thông tin dưới đây để trả lời các câu từ 109 đến 110:

Thực hiện Nghị quyết Hội nghị Trung ương lần thứ 21 của Đảng, từ cuối năm 1973, quân dân ta ở miền Nam không những kiên quyết đánh trả địch, bảo vệ vùng giải phóng, mà còn chủ động mở những cuộc tiến công địch tại những căn cứ xuất phát các cuộc hành quân của chúng, mở rộng vùng giải phóng.

Cuối năm 1974 - đầu năm 1975, ta mở đợt hoạt động quân sự ở vùng đồng bằng sông Cửu Long và Đông Nam Bộ. Quân ta đã giành thắng lợi vang dội trong chiến dịch đánh Đường 14 - Phước Long (từ ngày 12 – 12 – 1974 đến ngày 6-1-1975), loại khỏi vòng chiến đấu 3 000 địch, giải phóng Đường 14, thị xã và toàn tỉnh Phước Long với 50.000 dân.

Sau chiến thắng này của ta, chính quyền Sài Gòn phản ứng mạnh và đưa quân đến hòng chiếm lại, nhưng đã thất bại. Mĩ chỉ phản ứng yếu ớt, chủ yếu dùng áp lực đe doạ từ xa.

Thực tế thắng lợi của ta ở Phước Long, phản ứng của Mĩ và chính quyền Sài Gòn sau đó cho thấy rõ sự lớn mạnh và khả năng thắng lớn của quân ta, sự suy yếu và bất lực của quân đội Sài Gòn, về khả năng can thiệp trở lại bằng quân sự rất hạn chế của Mĩ.

Phối hợp với đấu tranh quân sự, nhân dân ta ở miền Nam đẩy mạnh đấu tranh chính trị, ngoại giao nhằm tố cáo hành động của Mỹ và chính quyền Sài Gòn vi phạm Hiệp định, phá hoại hoà bình, hoà hợp dân tộc; nêu cao tính chất chính nghĩa cuộc chiến đấu của nhân dân ta, đòi lật đổ chính quyền Nguyễn Văn Thiệu, thực hiện các quyền tự do dân chủ.

(Nguồn: SGK Lịch sử 12, trang 191)

Thực hiện Nghị quyết Hội nghị Trung ương lần thứ 21 của Đảng, từ cuối năm 1973, quân dân ta ở miền Nam

A. chủ động đánh địch và mở hàng loạt các cuộc tiến công địch ở đồng bằng sông Cửu Long.

B. kiên quyết đánh trả địch, bảo vệ vùng giải phóng và đồng loạt mở các cuộc tiến công địch.

C. kiên quyết đánh trả địch, bảo vệ vùng giải phóng và chủ động mở những cuộc tiến công địch.

D. chủ động đánh địch và mở hàng loạt các cuộc tiến công địch ở Đông Nam Bộ.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hàm số $y = x^{3} - 3 x^{2} - 2$ . Hệ số góc của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ $x = 2$ là:

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với \[A(1;0;0),{\mkern 1mu} {\mkern 1mu} B(3;2;4),{\mkern 1mu} C(0;5;4)\]. Tìm tọa độ điểm M thuộc mặt phẳng (Oxy) sao cho $| \vec{M A} + \vec{M B} + 2 \vec{M C} |$ nhỏ nhất.

A. \[M(1;3;0)\]

B. \[M(1; - 3;0)\]

C. \[M(3;1;0)\]

D. \[M(2;6;0)\]

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Mạng lưới điện sinh hoạt ở Việt Nam có điện áp hiệu dụng thường là 220V, còn ở Nhật Bản thì giá trị này là 110V. Chiếc đài radio Sony được xách tay từ Nhật Bản về Việt Nam, để dùng bình thường người ta phải dùng bộ sạc (máy biến áp nhỏ). Tỉ số vòng dây cuộn thứ cấp và sơ cấp của máy biến áp là k. Máy biến áp này là

A. máy hạ áp, k = 0,5.

B. máy hạ áp, k = 0,2.

C. máy tăng áp, k = 2.

D. máy tăng áp, k = 5.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Trong những năm 1945-1946, nước Việt Nam Dân chủ Cộng hòa có thuận lợi nào sau đây?

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng \(\left( P \right):x + 2y - 2z + 3 = 0\) và \(\left( Q \right):x + 2y - 2z - 1 = 0\). Khoảng cách giữa hai mặt phẳng (P) và (Q) là:

Cho hàm số $y = x^{3} - 3 x^{2} - 2$ . Hệ số góc của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ \(x = 2\) là:

Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với \[A(1;0;0),{\mkern 1mu} {\mkern 1mu} B(3;2;4),{\mkern 1mu} C(0;5;4)\]. Tìm tọa độ điểm M thuộc mặt phẳng (Oxy) sao cho $| \vec{M A} + \vec{M B} + 2 \vec{M C} |$ nhỏ nhất.

Trong những năm 1945-1946, nước Việt Nam Dân chủ Cộng hòa có thuận lợi nào sau đây?

Trong không gian Oxyz, cho mặt cầu (S):x2+y2+z2+2⁢x-4⁢y-2⁢z+92=0 và hai điểm \(A(0;2;0)\) \(,B(2; - 6; - 2)\). Điểm \(M\left( {a;b;c} \right)\) thuộc \(\left( S \right)\) thỏa mãn tích M⁢A→⁢ ⋅M⁢B→ có giá trị nhỏ nhất. Tổng \(a + b + c\) bằng

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng \(\left( P \right):x + 2y - 2z + 3 = 0\) và \(\left( Q \right):x + 2y - 2z - 1 = 0\). Khoảng cách giữa hai mặt phẳng (P) và (Q) là:

Cho hàm số y=x3-3⁢x2-2. Hệ số góc của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ \(x = 2\) là:

Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với \[A(1;0;0),{\mkern 1mu} {\mkern 1mu} B(3;2;4),{\mkern 1mu} C(0;5;4)\]. Tìm tọa độ điểm M thuộc mặt phẳng (Oxy) sao cho |M⁢A→⁢⁢ +M⁢B→⁢⁢ +2⁢M⁢C→| nhỏ nhất.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hàm số $y = x^{3} - 3 x^{2} - 2$ . Hệ số góc của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ \(x = 2\) là:

Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với \[A(1;0;0),{\mkern 1mu} {\mkern 1mu} B(3;2;4),{\mkern 1mu} C(0;5;4)\]. Tìm tọa độ điểm M thuộc mặt phẳng (Oxy) sao cho $| \vec{M A} + \vec{M B} + 2 \vec{M C} |$ nhỏ nhất.