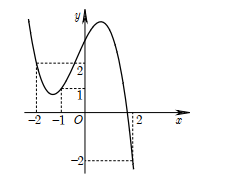
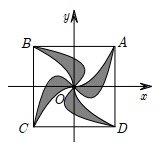
Mặt sàn của một thang máy có dạng hình vuông ABCD cạnh 2m được lát gạch màu trắng và trang trí bởi một hình 4 cánh giống nhau màu sẫm. Khi đặt trong hệ toạ độ Oxy với O là tâm hình vuông sao cho A(1; 1) như hình vẽ bên thì các đường cong OA có phương trình $y=x^2$ và $y=a{x}^3+bx.$ Tính giá trị ab biết rằng diện tích trang trí màu sẫm chiếm $\frac{1}{3}$ diện tích mặt sàn.

Ta có $u_1.u_3=u_2^2\Rightarrow u_1=\frac{u_2^2}{u_3}=\frac{9}{6}=\frac{3}{2}.$

Chọn C.

Vì $z_1,z_2$ là hai nghiệm phức của phương trình $z^2+bz+c=0$ nên $z_2=\overline{z_1}.$

Khi đó ta có $\left|z_2-8-6i\right|=4\iff \left|\overline{z_1}-8-6i\right|=4\iff \left|z_1-8+6i\right|=4.$

Gọi M là điểm biểu diễn số phức $z_1$

$\Rightarrow M$ vừa thuộc đường tròn $\left(C_1\right)$ tâm $I_1\left(4;-3\right),$ bán kính $R_1=1$ và đường tròn $\left(C_2\right)$ tâm $I_2\left(8;-6\right),$ bán kính $R_2=4.$

$\Rightarrow m\in \left(C_1\right)\cap \left(C_2\right).$

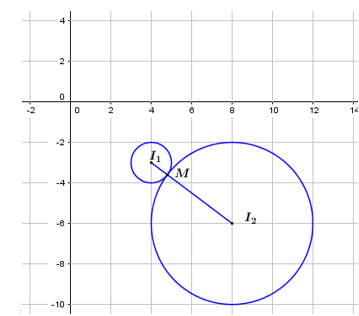
Ta có $I_1{I}_2=\sqrt{4^2+3^2}=5=R_1+R_2\Rightarrow \left(C_1\right)$ và $\left(C_2\right)$ tiếp xúc ngoài.

Do đó có duy nhất 1 điểm M thỏa mãn, tọa độ điểm M là nghiệm của hệ $\left\{\begin{array}{l}{x}^2+y^2-8x+6y+24=0\\ x^2+y^2-16x+12y+84=0\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\frac{24}{5}\\ y=-\frac{18}{5}\end{array}\right.\Rightarrow M\left(\frac{24}{5};-\frac{18}{5}\right)\Rightarrow z_1=\frac{24}{5}-\frac{18}{5}i$ là nghiệm của phương trình $z^2+bz+c=0$

$\Rightarrow z_2=\frac{24}{5}+\frac{18}{5}i$ cũng là nghiệm của phương trình $z^2+bz+c=0$

Áp dụng đinh lí Vi-ét ta có $z_1+z_2=-b=\frac{48}{5}\Rightarrow b=-\frac{48}{5},z_1{z}_2=c=36.$

Vậy $5b+c=-48+36=-12.$

Chọn B.