Đố vui.

Số 2 đã trải qua hành trình thú vị và bị biến đổi sau khi đi qua chiếc hộp đen.

Bác thợ máy đã giải mã hộp đen cho một số x bất kì như sau:

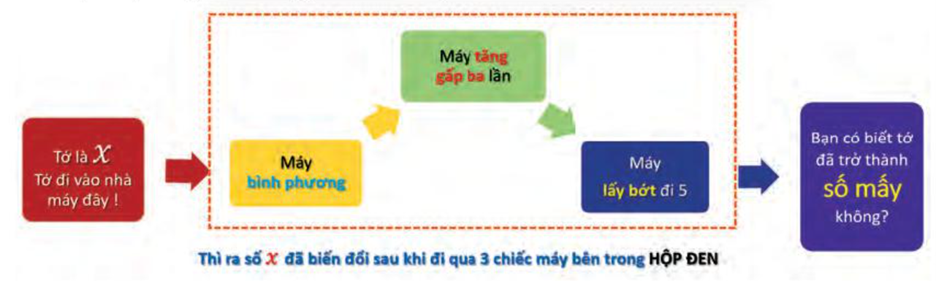
Bên trong hộp đen là một đoạn chương trình được cài đặt sẵn. Ta xem đoạn chương trình này như một hàm số f(x). Hãy viết biểu thức của f(x) để mô tả sự biến đổi đã tác động lên x.

a)

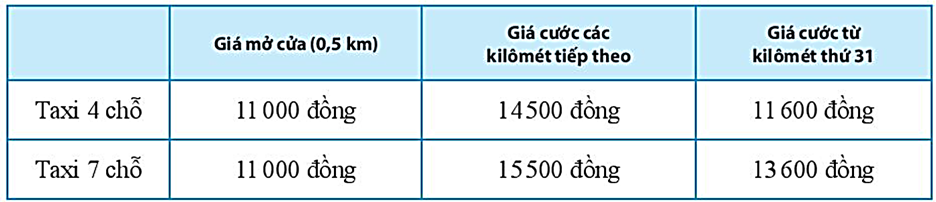
i) Khi di chuyển bằng xe taxi 4 chỗ:

Nếu x ≤ 0,5 thì số tiền hành khách phải trả là: 11 000x (nghìn đồng).

Nếu 0,5 < x < 31 thì số tiền hành khách phải trả là: 11 000.0,5 + 14 500(x – 0,5) = 14 500x – 1 750 (nghìn đồng).

Nếu x ≥ 31 thì số tiền hành khách phải trả là: 11 000.0,5 + 14 500(31 – 0,5) + 11 600(x – 31) = 11 600x + 88 150 (nghìn đồng).

Vậy hàm số f(x) được xác định như sau:

$f\left(x\right)=\left\{\begin{array}{l}11000xkhix\le 0,5\\ 14500x-1750khi0<x<31\\ 11600x+88150khix\ge 31\end{array}\right.$.

ii) Khi di chuyển bằng xe taxi 7 chỗ:

Nếu x ≤ 0,5 thì số tiền hành khách phải trả là: 11 000x (nghìn đồng).

Nếu 0,5 < x < 31 thì số tiền hành khách phải trả là: 11 000.0,5 + 15 500(x – 0,5) = 15 500x – 2 250 (nghìn đồng).

Nếu x ≥ 31 thì số tiền hành khách phải trả là: 11 000.0,5 + 15 500(31 – 0,5) + 13 600(x – 31) = 13 600x + 56 650 (nghìn đồng).

Vậy hàm số g(x) được xác định như sau:

$g\left(x\right)=\left\{\begin{array}{l}11000xkhix\le 0,5\\ 15500x-2250khi0<x<31\\ 13600x+56650khix\ge 31\end{array}\right.$.

b) Có tất cả 30 hành khách nếu đặt xe 4 chỗ thì cần 8 xe, còn nếu đặt xe 7 chỗ thì cần 5 xe.

Với x ≤ 0,5, ta có:

Số tiền hành khách phải trả khi thuê xe 4 chỗ là: 8.11 000x = 88 000x (nghìn đồng).

Số tiền hành khách phải trả khi thuê xe 7 chỗ là: 5.11 000x = 55 000x (nghìn đồng).

Vì 55 000 < 88 000 nên 55 000x < 88 000x.

Do đó nếu quãng đường di chuyển nhỏ hơn 0,5km thì nên đặt xe 7 chỗ thì có lợi hơn.

Với 0,5 < x < 31, ta có:

Số tiền hành khách phải trả khi thuê xe 4 chỗ là: 8.(14 500x – 1 750) = 116 000x – 14 000 (nghìn đồng).

Số tiền hành khách phải trả khi thuê xe 7 chỗ là: 5.(15 500x – 2 250) = 77 500x – 11 250 (nghìn đồng).

Ta có: 44 000 < 116 000x – 14 000 < 3 582 000 và 27 500 < 77 500x – 11 250 < 2 391 250.

Do đó nếu quãng đường di chuyển lớn hơn 0,5km và nhỏ hơn 31km thì nên đặt xe 7 chỗ thì có lợi hơn.

Với x ≥ 31, ta có:

 Số tiền hành khách phải trả khi thuê xe 4 chỗ là: 8.(11 600x + 88 150) = 92 800x + 705 200 (nghìn đồng).

Số tiền hành khách phải trả khi thuê xe 7 chỗ là: 5.(13 600x + 56 650) = 68 000x + 183 250 (nghìn đồng).

Ta có: 92 800x + 705 200 ≥ 68 000x + 183 250 .

Do đó nếu quãng đường di chuyển lớn hơn 0,5km và nhỏ hơn 31km thì nên đặt xe 7 chỗ thì có lợi hơn.

Vậy nếu đặt xe taxi cho 30 hành khách thì nên đặt toàn bộ xe 7 chỗ thì có lợi hơn.

a)

Tập xác định D = $ℝ$.

Lấy $x_1$,$x_2$ là hai số thực tùy ý thỏa mãn $x_1$ < $x_2$, ta có:

f(x₁) – f(x₂) = (-5$x_1$+ 2) – (-5$x_2$+ 2) = -5x₁ + 2 + 5x₂ – 2 = -5x₁ + 5x₂ = 5(x₂ – x₁)

Vì $x_1$ < $x_2$ $\Rightarrow$ 5(x₂ – x₁) > 0 $\Rightarrow$ f($x_1$) – f($x_2$) > 0 hay f($x_1$) > f($x_2$).

Vậy hàm số nghịch biến (giảm) trên $ℝ$

b)

Tập xác định D = $ℝ$.

Lấy $x_1$,$x_2$ là hai số thực tùy ý thỏa mãn $x_1$ < $x_2$, ta có:

f($x_1$) – f($x_2$) = - x₁² – (-x₂²) = ${x_2}^2-{x_1}^2$ = (x₂ – x₁)(x₂ + x₁)

+) Với x₁, x₂ ∈ (-∞; 0) và x₁ < x₂, khi đó: x₁ + x₂ < 0 và x₂ – x₁ > 0

Do đó, f(x₁) – f(x₂) < 0 $\Rightarrow$f(x₁) < f(x₂), nên hàm số f(x) đồng biến trên khoảng (-∞; 0).

+) Với x₁,  x₂ ∈ (-∞; 0) và x₁ < x₂, khi đó: x₁ + x₂ > 0 và x₂ – x₁ > 0

Do đó, f(x₁) – f(x₂) > 0 $\Rightarrow$f(x₁) > f(x₂) nên hàm số f(x) nghịch biến trên khoảng (0; +∞).

Vậy hàm số f(x) = -$x^2$đồng biến trên khoảng (-∞; 0) và nghịch biến trên khoảng (0; +∞).