Câu hỏi:

02/06/2022 8,572

Biết rằng hàm số y = 2x² + mx + n giảm trên khoảng (-∞; 1), tăng trên khoảng (1; + ∞) và có tập giá trị là [9; +∞). Xác định giá trị của m và n.

Xem lời giải

Câu hỏi trong đề: Bài tập cuối chương III có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Ta có giảm trên khoảng (-∞; 1), tăng trên khoảng (1; + ∞) và có tập giá trị là [9; +∞) nên điểm đỉnh S có tọa độ (1; 9).

Do đó x_S = $- \frac{b}{2 a} = 1 \Leftrightarrow - \frac{m}{2.2} = 1 \Leftrightarrow m = - 4$ .

Và y_S= 2.1² + m.1 + n = 9 ⇔ 2 + (-4) + n = 9 ⇔ n = 11.

Vậy với m= -4 và n = 11 thì hàm số đã cho thỏa mãn điều kiện bài toán.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Nhảy bungee là một trò chơi mạo hiểm. Trong trò chơi này, người chơi đứng ở vị trí trên cao, thắt dây an toàn vả nhảy xuống. Sợi dây này có tính đàn hồi và được tính toán chiều dài để nó kéo người chơi lại khi gần chạm đất (hoặc mặt nước).

Chiếc cầu trong Hình 1 có bộ phận chống đỡ dạng parabol. Một người thực hiện một cú nhảy bungee từ giữa cầu xuống với dây an toàn. Người này cần trang bị sợi dây an toàn dài bao nhiêu mét? Biết rằng chiều dài của sợi dây đó bằng một phần ba khoảng cách từ vị trí bắt đầu nhảy đến mặt nước.

Xem đáp án

Lời giải

Ta có sơ đồ sau:

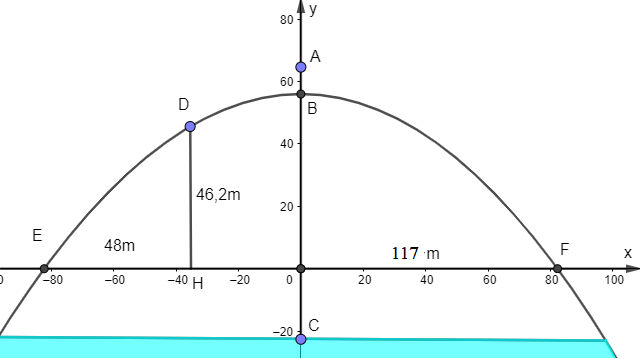
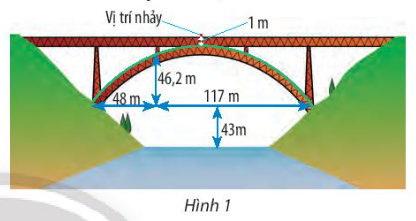
Media VietJack

Điểm A là vị trí nhảy của người đó, E và F là chân bộ phận chống đỡ cầu.

Vì bộ phận chống đỡ cầu có dạng parabol (P) nên có phương trình: y = ax² + bx + c.

Đoạn EF = 48 + 117 = 165 m, OE = EF : 2 = 165:2 = 82,5m

⇒ OH = OE – EH = 34,5 m

Khi đó tọa độ D(34,5; 46,2), E(-82,5; 0) và F(82,5; 0).

Vì các điểm D, E, F thuộc đồ thị hàm số (P) nên ta có hệ phương trình:

$\{\begin{cases} a . {(- 82, 5)}^{2} + b . (- 82, 5) + c = 0 \\ a . {(82, 5)}^{2} + b . (82, 5) + c = 0 \\ a . {(34, 5)}^{2} + b . (34, 5) + c = 46, 2 \end{cases} \Leftrightarrow \{\begin{cases} a = - \frac{77}{9360} \\ b = 0 \\ c = \frac{46565}{832} \end{cases}$

Suy ra parabol cần tìm là: $y = - \frac{77}{9360} x^{2} + \frac{46565}{832}$ .

Điểm B là điểm đỉnh nên có x_B = 0 và y_B = $- \frac{77}{9360} {.0}^{2} + \frac{46565}{832} = \frac{46565}{832}$

Do đó OB = $\frac{46565}{832}$ (m)

Khoảng cách từ vị trí nhảy đến mặt nước là:

AB + OB + OC = 1 + $\frac{46565}{832}$ + 43 ≈ 99,97 m.

Độ dài sợi dây là: 99,97: 3 = 33,32 m.

Vậy độ dài sợi dây là 33,32 m.

Câu 2

Giả sử một máy bay cứu trợ đang bay theo phương ngang và bắt đầu thả hàng từ độ cao 80m, lúc đó máy bay đang bay với vận tốc 50m/s. Để thùng hàng hỗ trợ rơi trúng vị trí được chọn, máy bay cần thả hàng ở vị trí nào? Biết rằng nếu chọn gốc tọa độ là hình chiếu trên mặt đất của vị trí hàng cứu trợ bắt đầu được thả, thì tọa độ của hàng cứu trợ được cho bởi hệ sau:

$\{\begin{cases} x = v_{0} t \\ y = h - \frac{1}{2} g t^{2} \end{cases}$

Trong đó, v₀ là vận tốc ban đầu và h là độ cao tính từ khi hàng rời máy bay.

Lưu ý: Chuyển động này được xem là chuyển động ném ngang.

Xem đáp án

Lời giải

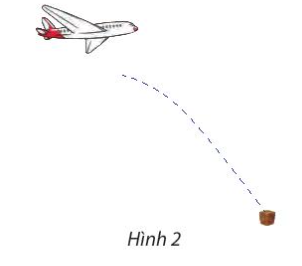
Gọi A là vị trí bắt đầu thả hàng, C là vị trí được chọn để nhận thùng hàng hỗ trợ.

Ta có O là hình chiếu của A trên mặt đất nên ta có hình vẽ sau:

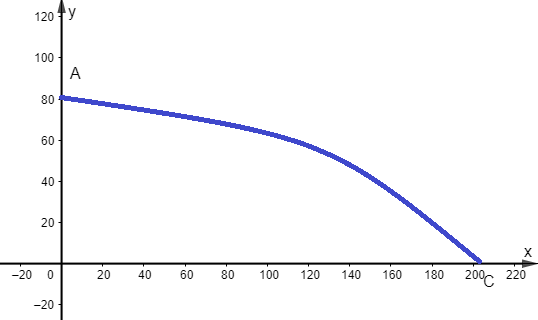
Media VietJack

Tọa độ điểm C là nghiệm của hệ phương trình:

$\{\begin{cases} x_{C} = v_{0} t \\ y_{C} = h - \frac{1}{2} g t^{2} \end{cases}$ với h = 80m, g = 9,8m/s², v₀ = 50m/s.

Do C ở mặt đất nên tung độ của C là y_C = 0. Khi đó ta có hệ phương trình:

$\{\begin{cases} x_{C} = 50. t \\ 0 = 80 - \frac{1}{2} .9, 8. t^{2} \end{cases} \Leftrightarrow \{\begin{cases} x_{C} = 50. t \\ 0 = 80 - \frac{1}{2} .9, 8. t^{2} \end{cases} \Leftrightarrow \{\begin{cases} x_{C} \approx 202, 03 \\ t = \frac{20 \sqrt{2}}{7} \end{cases} \Rightarrow \{\begin{cases} x_{C} \approx 202, 03 \\ y_{C} = 0 \end{cases}$

Vậy vị trí được chọn để nhận thùng hàng hỗ trợ có tọa độ là (202,03; 0).

Câu 3

Tìm điều kiện của m để mỗi hàm số sau đây là một hàm số bậc hai:

a) y = (1 – 3m)x² + 3;

b) y = (4m – 1)(x – 7)²;

c) y = 2(x² + 1) + 11 – m.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Tìm tập xác định của các hàm số sau:

a) y = 4x² – 1;

b) $y = \frac{1}{x^{2} + 1};$

c) $y = 2 + \frac{1}{x} .$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Vẽ đồ thị các hàm số sau:

a) y = x² – 4x + 3;

b) y = - x² – 4x + 5;

c) y = x² – 4x + 5;

d) y = -x² – 2x – 1.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Một vận động viên chạy xe đạp trong 1 giờ 30 phút đầu với vận tốc trung bình là 42km/h. Sau đó người này nghỉ tại chỗ 15 phút và tiếp tục đạp xe 2 giờ liền với vận tốc 30km/h.

a) Hãy biểu thị quãng đường s (tính bằng ki lô mét) mà người này đi được sau t phút bằng một hàm số.

b) Vẽ đồ thị biểu diễn hàm số s theo t.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Biết rằng hàm số y = 2x2 + mx + n giảm trên khoảng (-∞; 1), tăng trên khoảng (1; + ∞) và có tập giá trị là [9; +∞). Xác định giá trị của m và n.

Bình luận

Tìm điều kiện của m để mỗi hàm số sau đây là một hàm số bậc hai: a) y = (1 – 3m)x2 + 3; b) y = (4m – 1)(x – 7)2; c) y = 2(x2 + 1) + 11 – m.

Tìm tập xác định của các hàm số sau: a) y = 4x2 – 1; b) y=1x2+1; c) y=2+1x.

Vẽ đồ thị các hàm số sau: a) y = x2 – 4x + 3; b) y = - x2 – 4x + 5; c) y = x2 – 4x + 5; d) y = -x2 – 2x – 1.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Biết rằng hàm số y = 2x² + mx + n giảm trên khoảng (-∞; 1), tăng trên khoảng (1; + ∞) và có tập giá trị là [9; +∞). Xác định giá trị của m và n.

Tìm điều kiện của m để mỗi hàm số sau đây là một hàm số bậc hai:

a) y = (1 – 3m)x² + 3;

b) y = (4m – 1)(x – 7)²;

c) y = 2(x² + 1) + 11 – m.

Tìm tập xác định của các hàm số sau:

a) y = 4x² – 1;

b) $y = \frac{1}{x^{2} + 1};$

c) $y = 2 + \frac{1}{x} .$

Vẽ đồ thị các hàm số sau:

a) y = x² – 4x + 3;

b) y = - x² – 4x + 5;

c) y = x² – 4x + 5;

d) y = -x² – 2x – 1.