Câu hỏi:

12/07/2024 2,910

1) Giải hệ phương trình \(\left\{ \begin{array}{l}\left( {2x + 3y - 2} \right)\left( {x - 5y - 3} \right) = 0\\x - 3y = 1\end{array} \right.\)

2) Giải phương trình: \(3\sqrt {x - 2} - \sqrt {{x^2} - 4} = 0\).

3) Cho phương trình \(\left( {2m - 1} \right){x^2} - 2mx + 1 = 0\). Tìm m để phương trình trên có nghiệm thuộc khoảng \(\left( { - 1;0} \right)\)?

Xem lời giải

Câu hỏi trong đề: Đề ôn thi vào 10 môn Toán có đáp án (Mới nhất) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

1) Hệ Phương trình tương đương với: \(\left\{ \begin{array}{l}\left[ \begin{array}{l}2x + 3y - 2 = 0\\x - 5y - 3 = 0\end{array} \right.\\x - 3y = 1\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}2x + 3y - 2 = 0\\x - 3y = 1\end{array} \right. \vee \left\{ \begin{array}{l}x - 5y - 3 = 0\\x - 3y = 1\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}2\left( {1 + 3y} \right) + 3y - 2 = 0\\x = 1 + 3y\end{array} \right. \vee \left\{ \begin{array}{l}\left( {1 + 3y} \right) - 5y - 3 = 0\\x = 1 + 3y\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}9y = 0\\x = 1 + 3y\end{array} \right. \vee \left\{ \begin{array}{l} - 2y - 2 = 0\\x = 1 + 3y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 0\end{array} \right. \vee \left\{ \begin{array}{l}x = - 2\\y = - 1\end{array} \right.\)

Vậy hệ phương trình có nghiệm là: \(\left( {x;y} \right) = \left( {1;0} \right),\,\,\left( { - 2; - 1} \right)\)

2) Điều kiện: \(\left\{ \begin{array}{l}x - 2 \ge 0\\{x^2} - 4 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\\left[ \begin{array}{l}x \le - 1\\x \ge 2\end{array} \right.\end{array} \right. \Leftrightarrow x \ge 2\)

Phương trình tương đương \[3\sqrt {x - 2} - \sqrt {\left( {x - 2} \right)\left( {x + 2} \right)} = 0\]

\( \Leftrightarrow \sqrt {x - 2} \left( {3 - \sqrt {x + 2} } \right) = 0 \Leftrightarrow \left[ \begin{array}{l}\sqrt {x - 2} = 0\\3 - \sqrt {x + 2} = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\\x + 2 = 9\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 7\end{array} \right.\) (thõa mãn điều kiện)

3) + Xét \(2m - 1 = 0 \Leftrightarrow m = \frac{1}{2}\)phương trình trở thành: \( - x + 1 = 0 \Leftrightarrow x = 1\), không thuộc khoảng \(\left( { - 1;0} \right)\).

+ Xét \(2m - 1 \ne 0 \Leftrightarrow m \ne \frac{1}{2}\), khi đó ta có

\(\Delta ' = {m^2} - \left( {2m - 1} \right).1 = {m^2} - 2m + 1 = {\left( {m - 1} \right)^2} \ge 0,\,\,\forall m\); nên phương trình có nghiệm với mọi m.

Suy ra \(\sqrt {\Delta '} = m - 1\).

Phương trình có nghiệm là: \(\left\{ \begin{array}{l}x = \frac{{m + \left( {m - 1} \right)}}{{2m - 1}} = 1 \notin \left( { - 1;0} \right)\\x = \frac{{m - \left( {m - 1} \right)}}{{2m - 1}} = \frac{1}{{2m - 1}}\end{array} \right.\)

Theo bài ra, ta có: \( - 1 < \frac{1}{{2m - 1}} < 0 \Leftrightarrow \left\{ \begin{array}{l} - 1 < \frac{1}{{2m - 1}}\\\frac{1}{{2m - 1}} < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\frac{{2m}}{{2m - 1}} > 0\\2m - 1 < 0\end{array} \right. \Leftrightarrow m < 0\)

Vậy phương trình có nghiệm thuộc khoảng \(\left( { - 1;0} \right)\) khi và chỉ khi \(m < 0\).

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho đường tròn \(\left( {O;R} \right)\) có đường kính AB. Vẽ dây cung CD vuông góc với AB (CD không đi qua tâm O). Trên tia đối của tia BA lấy điểm S; SC cắt \(\left( {O;R} \right)\) tại điểm thứ hai là M.

1) Chứng minh \(\Delta SMA\) đồng dạng với \(\Delta SBC\).

2) Gọi H là giao điểm của MAvà BC; K là giao điểm của MD và AB. Chứng minh BMHK là tứ giác nội tiếp và \(HK//CD\).

3) Chứng minh: \(OK.OS = {R^2}\).

Xem đáp án

Lời giải

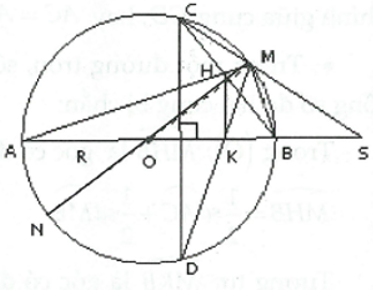
Cho đường tròn (O;R) có đường kính AB. Vẽ dây cung CD vuông góc với AB (CD không đi qua tâm O). Trên tia đối của tia BA (ảnh 1)

1) \(\Delta SBC\) và \(\Delta SMA\) có:

\(\widehat {BSC} = \widehat {MSA}\), \(\widehat {SCB} = \widehat {SAM}\) (góc nội tiếp cùng chắn )

\( \Rightarrow \Delta DBC\) đồng dạng với \(\Delta SMA\).

Nhận xét: Bài toán chứng minh hai tam giác đồng dạng theo trường hợp góc – góc.

2) Vì \(AB \bot CD\) nên .

Suy ra: \(\widehat {MHB} = \widehat {MKB}\) (vì cùng bằng )

\( \Rightarrow \) Tứ giác BMHK nội tiếp được đường tròn \( \Rightarrow \widehat {HMB} + \widehat {HKB} = 180^\circ \). (1)

Lại có: \(\widehat {HMB} = \widehat {AMB} = 90^\circ \) (2) (góc nội tiếp chắn nửa đường tròn)

Từ (1) (2) suy ra \(\widehat {HKB} = 90^\circ \) do đó \(HK//CD\) (cùng vuông góc với AB).

Nhận xét: Bài toán chứng minh hai đường thẳng song song bằng cách chứng minh chúng cùng vuông góc với một đường thẳng thứ ba.

3) Vẽ đường kính MN suy ra .

Ta có:

Mà và nên \(\widehat {OSM} = \widehat {OMK}\)

\( \Rightarrow \Delta OSM\) đồng dạng với \(\Delta OMK\)

\( \Rightarrow \frac{{OS}}{{OM}} = \frac{{OM}}{{OK}} \Rightarrow OK.OS = {R^2}\)

Nhận xét: Bài toán chứng minh một đẳng thức bằng cách chứng minh tam giác đồng dạng.

Câu 2

1) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình.

Một thửa ruộng hình chữ nhật, nếu tăng chiều dài thêm 2m, chiều rộng thêm 3m thì diện tích tăng thêm 100m2. Nếu giảm cả chiều dài và chiều rộng đi 2m thì diện tích giảm đi 68m2. Tính diện tích thửa ruộng đó.

2) Xác định a, b để đường thẳng \(\left( d \right):ax + b\) cắt trục tung tại điểm có tung độ bằng \( - 2\) và cắt đồ thị \(\left( P \right):y = \frac{1}{4}{x^2}\) tại điểm có hoành độ bằng 2.

Xem đáp án

Lời giải

1) Gọi chiều dài của thửa ruộng là \[x\] (m).

Chiều rộng là y (m).

Điều kiện:\[x,{\rm{ }}y > 0\] .

Diện tích thửa ruộng là \(x.y\).

Nếu tăng chiều dài thêm 2m, chiều rộng thêm 3 m thì diện tích thửa ruộng lúc này là: \(\left( {x + 2} \right)\left( {y + 3} \right)\) và diện tích tăng thêm 100m2, tức là \(\left( {x + 2} \right)\left( {y + 3} \right) = xy + 100\) (1)

Nếu giảm cả chiều dài và chiều rộng 2m thì diện tích thửa ruộng còn lại là \(\left( {x - 2} \right)\left( {y - 2} \right)\) và diện tích giảm đi 68m2, tức là \(\left( {x - 2} \right)\left( {y - 2} \right) = xy - 68\) (2)

Từ (1) và (2), ta có hệ phương trình \(\left\{ \begin{array}{l}\left( {x + 2} \right)\left( {y + 3} \right) = xy + 100\\\left( {x - 2} \right)\left( {y - 2} \right) = xy - 68\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}xy + 3x + 2y + 6 = xy + 100\\xy - 2x - 2y + 4 = xy - 68\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x + 2y = 94\\2x + 2y = 72\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 22\\x + y = 36\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 22\\y = 14\end{array} \right.\)

Vậy diện tích thửa ruộng là: \(S = 22.14 = 308\left( {{m^2}} \right)\)

2) Đường thẳng \(\left( d \right):y = ax + b\) cắt trục tung tại điểm có tung độ bằng \( - 2\), nên ta có phưong trình: \( - 2 = a.0 + b \Leftrightarrow b = - 2\)

Suy ra đường thẳng \(\left( d \right)\) có dạng: \(y = ax - 2\).

Đường thẳng \(\left( d \right):y = ax - 2\) cắt đồ thị \(\left( P \right):y = \frac{1}{4}{x^2}\) tại điểm có hoành độ bằng 2, nên ta có phương trình:\(a.2 - 2 = \frac{1}{4}{.2^2} \Leftrightarrow a = \frac{3}{2}\)

Vậy đường thẳng \(\left( d \right)\) là: \(y = \frac{3}{2}x - 2\).

Câu 3