✕

✨ Đăng kí VIP để truy cập không giới hạn. Đăng ký ngay

Câu hỏi:

14/01/2020 68,125

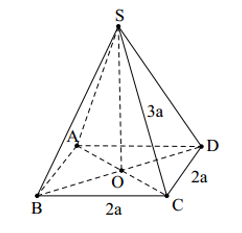
Cho hình chóp đều S ABCD. có cạnh đáy bằng 2a cạnh bên bằng 3a. Khoảng cách từ A đến (SCD) bằng

A. $\frac{a \sqrt{14}}{3}$

B. $\frac{a \sqrt{14}}{4}$

C. $a \sqrt{14}$

D. $\frac{a \sqrt{14}}{2}$

Xem lời giải

Câu hỏi trong đề: 187 Bài trắc nghiệm Khối đa diện từ đề thi đại học có đáp án chi tiết !!

Quảng cáo

Trả lời:

Giải bởi Vietjack

Chọn D.

Do S.ABCD chóp đều nên đáy ABCD là hình vuông và SO $⊥$ (ABCD)

Ta có:

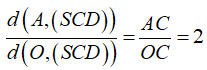
Xét tam giác ACD vuông tại D có

Xét tam giác SOC vuông tại O có:

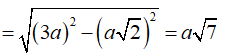
Do tứ diện S.OCD có 3 cạnh OS, OC, OD đôi một vuông góc

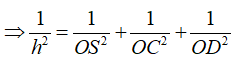
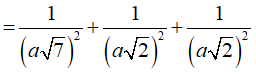
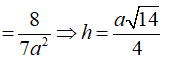
Vậy khoảng cách từ A đến (SCD) bằng $\frac{a \sqrt{14}}{2}$

Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình chóp S.ABCD có đáy hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a. Gọi M và N lần lượt là trung điểm của AD và SD. Số đo góc (MN,SC) bằng

A. $45^{o}$

B. $30^{o}$

C. $90^{o}$

D. $60^{o}$

Lời giải

Đáp án C

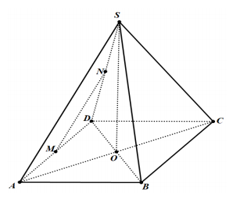
MN là đường trung bình của tam giác DAS nên MN//SA

Gọi O là tâm của hình vuông ABCD, vì SA=SC=SB=SD nên SO $⊥$ (ABCD)

Câu 2

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, BC = 2a. Cạnh bên SA = 2a và SA vuông góc với mặt phẳng đáy. Khoảng cách giữa SC và BD bằng :

A. $\frac{2 a}{3}$

B. $\frac{a \sqrt{3}}{2}$

C. $\frac{4 a}{3}$

D. $\frac{3 a}{2}$

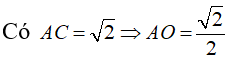
Lời giải

Chọn A.

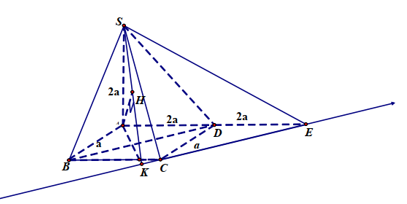
Trong mặt phẳng (ABCD), qua C kẻ CE//BD => BD//(SCE)

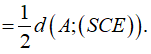
Từ A kẻ AK $⊥$ CE. Dễ dàng chứng minh được:

+ Tính AH: Áp dụng hệ thức lượng trong tam giác vuông SAK ta có:

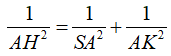
+ Tính AK

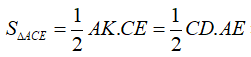
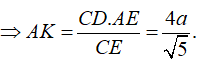
Suy ra:

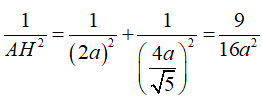
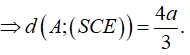
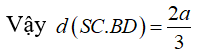
Câu 3

Cho hình chóp S.ABCD có đáy là hình vuông cạnh 3a, SA vuông góc với đáy, SB = 5a. Tính sin của góc giữa cạnh SC và mặt đáy (ABCD).

A. $\frac{2 \sqrt{2}}{3}$

B. $\frac{3 \sqrt{2}}{4}$

C. $\frac{3 \sqrt{17}}{17}$

D. $\frac{2 \sqrt{34}}{17}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hình chóp S ABC có đáy ABC là tam giác vuông tại A , cạnh bên SA vuông góc với (ABC). Gọi I là trung điểm cạnh AC , H là hình chiếu của I trên SC . Khẳng định nào sau đây đúng?

A. (SBC) $⊥$ (IHB)

B.(SAC) $⊥$ (SAB)

C.(SAC) $⊥$ (SAB)

D.(SBC) $⊥$ (SBC)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a, AA' $= \frac{3 a}{2}$ . Biết rằng hình chiếu vuông góc của A' lên (ABC) là trung điểm BC. Tính thể tích V của khối lăng trụ đó.

A. $V = a^{3}$

B. $V = \frac{2 a^{3}}{3}$

C. $V = \frac{3 a^{3}}{4 \sqrt{2}}$

D. $V = a^{3} \sqrt{\frac{3}{2}}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hình lăng trụ tam giác đều ABC.A’B’C’ có AB=2a, AA'=a $\sqrt{3}$ . Tính thể tích khối lăng trụ ABC.A’B’C’

A. 3 $a^{3}$

B. $a^{3}$

C. $\frac{a^{3}}{4}$

D. $\frac{3 a^{3}}{4}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »