Câu hỏi trong đề: Đề kiểm tra cuối kì 2 Toán 8 có đáp án ( Mới nhất) !!
Quảng cáo
Trả lời:
Ta có:
Û x2 + 25 = 0 hoặc
(vì x2 + 25 > 0 )
.
Do đó, tập nghiệm của phương trình đã cho là .
Vậy chọn đáp án C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
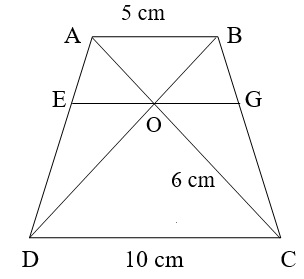
a) Ta có AB // CD, áp dụng định lý Ta-let: .
Do đó: OA . OD = OB . OC (đpcm).
b) Từ câu a suy ra:
(cm).
Do OE // DC nên theo hệ quả định lí Ta-let:
(cm).
Vậy OA = 3 cm, cm.
c) Do OE // AB, theo hệ quả định lý Ta-lét ta có: (1)
Do OE // CD, theo hệ quả định lý Ta-lét ta có: (2)
Cộng vế theo vế của (1) và (2) ta được: .
Suy ra hay (*)
Chứng minh tương tự, ta có: (**)
Từ (*) và (**) suy ra: (đpcm).
Lời giải

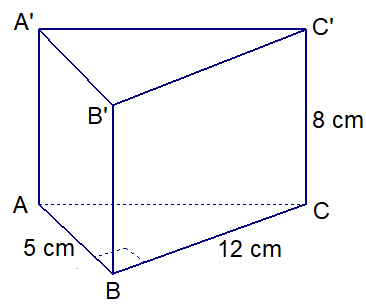
Độ dài hai cạnh góc vuông của đáy là 5 cm, 12 cm nên ∆ABC vuông tại B.
Theo định lý Py-ta-go, ta có:
(cm).
Diện tích xung quanh của lăng trụ là:
(5 + 12 + 13) . 8 = 240 (cm2).
Diện tích một đáy của lăng trụ là:
(cm2).
Thể tích của lăng trụ là:
30 . 8 = 240 (cm3).
Vậy hình lăng trụ có diện tích xung quanh là 240 cm2 và có thể tích là 240 cm3.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.