Câu hỏi:
06/12/2021 89,874Có thể chia một khối lập phương thành bao nhiêu khối tứ diện có thể tích bằng nhau mà các đỉnh của tứ diện cũng là đỉnh của hình lập phương?
Đáp án chính xác
Câu hỏi trong đề:
Bài tập Khối đa diện từ đề thi Đại học có lời giải chi tiết !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta chia hình lập phương thành 6 khối tứ diện bằng nhau như sau:
+) Chia khối lập phương ABCD. A’B’C’D’ thành hai khối lăng trụ tam giác bằng nhau: ABC.A’B’C’ và BCD.B’C’D’.
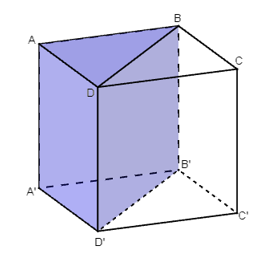
+) Tiếp đó, lần lượt chia khối lăng trụ ABD.A’B’D’ và BCD.B’C’D’ thành ba tứ diện: DABB’, DAA’B’ và DCBB’, DCC’B’, DD’C’B’.
+ Ta chứng minh được các khối tứ diện này bằng nhau như sau:
- Hai khối tứ diện DABB’ và DAA’B’ bằng nhau vì chúng đối xứng nhau qua mặt phẳng (DAB’) (1)
- Hai khối tứ diện DAA’B’ và DD’A’B’ bằng nhau vì chúng đối xứng nhau qua mặt phẳng (B’A’D) (2)
Từ (1) và (2) suy ra ba khối tứ diện DABB’, DAA’B’ và DD’A’B’ bằng nhau.
- Tương tự, ba khối tứ diện DCBB’, DCC’B’, DD’C’B’ cũng bằng nhau.
Vậy khối lập phương ABCD.A’B’C’D’ được chia thành sáu khối tứ diện bằng nhau.
Chọn D.
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình bát diện đều cạnh a. Gọi S là tổng diện tích tất cả các mặt của hình bát diện đó. Tính S.
Xem đáp án »
18/01/2020
107,649
Câu 3:
Cắt khối trụ bởi các mặt phẳng và ta được những khối đa diện nào?
Xem đáp án »
14/12/2021
48,425
Câu 4:
Một hình đa diện có các mặt là các tam giác có số mặt M và số cạnh C của đa diện đó thỏa mãn hệ thức nào dưới đây
Xem đáp án »
18/01/2020
38,642
Câu 6:
Một hình chóp có tất cả 2018 mặt. Hỏi hình chóp đó có bao nhiêu đỉnh?
Xem đáp án »
18/01/2020
29,029
Bình luận
🔥 Đề thi HOT:
-
53 câu Bài tập về Tính đơn điệu của hàm số có lời giải (P1)
-
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)
-
200 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số nâng cao (P1)
-
120 câu Bài tập Cực trị hàm số cơ bản, nâng cao có lời giải (P1)
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
-
124 câu Trắc nghiệm Ôn tập Toán 12 Chương 3 Hình học có đáp án (Phần 1)
-
250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số cơ bản (P1)
về câu hỏi!