Cho \(A = \frac{{3n + 1}}{{n - 2}}\) (n ≠ 2). Tìm \(n \in \mathbb{N}\) để biểu thức A đạt giá trị nguyên.
Cho \(A = \frac{{3n + 1}}{{n - 2}}\) (n ≠ 2). Tìm \(n \in \mathbb{N}\) để biểu thức A đạt giá trị nguyên.
Câu hỏi trong đề: Đề kiểm tra Giữa kì 2 Toán 7 có đáp án (Mới nhất) !!
Quảng cáo
Trả lời:
Với n ≠ 2, ta có: \(A = \frac{{3n + 1}}{{n - 2}} = \frac{{3(n - 2) + 7}}{{n - 2}} = 3 + \frac{7}{{n - 2}}\)
Để biểu thức A đạt giá trị nguyên hay \(3 + \frac{7}{{n - 2}} \in \mathbb{Z}\) thì \(\frac{7}{{n - 2}} \in \mathbb{Z}\).
Khi đó, n – 2 \( \in \) Ư(7) = {–1; 1; –7; 7}.
Ta có bảng sau:
|
n – 2 |
–1 |
1 |
–7 |
7 |
|
n |
1 (TM) |
3 (TM) |
–5 (loại vì \(n \in \mathbb{N}\)) |
9 (TM) |
Vậy để biểu thức A đạt giá trị nguyên thì n \( \in \) {1; 3; 9}.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
GT |
\(\widehat {xOy}\) nhọn; lấy \(A \in {\rm{Ox}}\), \(B \in Oy\): OA = OB. OI là tia phân giác \(\widehat {xOy}\) (\(I \in AB\)). Điểm C nằm giữa hai điểm O và I; OA = 5 cm, AB = 6cm. |
|
KL |
a) IA = IB. b) ΔABC là tam giác cân. c) Tính độ dài OI. |
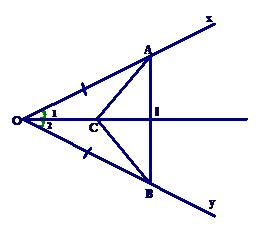
a) Xét ΔOIA và ΔOIB có:
OA = OB (gt)
\[{\widehat O_1} = {\widehat O_2}\] (vì OI là tia phân giác \(\widehat {xOy}\))
Cạnh OI chung.
Do đó ΔOIA = ΔOIB (c.g.c)
Suy ra IA = IB (hai cạnh tương ứng).
b) Xét ΔOCA và ΔOCB có:
OA = OB (gt)
\[{\widehat O_1} = {\widehat O_2}\] (vì OI là tia phân giác \(\widehat {xOy}\))
Cạnh OC chung.
Do đó ΔOCA = ΔOCB (c.g.c)
Do đó CA = CB (hai cạnh tương ứng)
Vậy tam giác ABC cân tại A.
c) ΔOBC có OI là đường trung tuyến cũng là đường phân giác, đường cao.
Áp dụng định lý Py-ta-go vào ΔAOI vuông tại I, ta có:
OA2 = OI2 + IA2
Suy ra: OI2 = OA2 – IA2 = 52 – 32 = 25 – 9 = 16
Do đó: .
Lời giải
a) Bảng “tần số”:
|
Chiều cao (x) |
138 |
139 |
140 |
141 |
143 |
145 |
150 |
|
|
Tần số (n) |
2 |
3 |
4 |
5 |
2 |
3 |
1 |
N = 20 |
b) Thầy giáo đã đo chiều cao của 20 bạn.
c) Số bạn có chiều cao thấp nhất là hai bạn.
d) Có hai bạn cao 143 cm.
e) Số các giá trị khác nhau của dấu hiệu là 7.
f) Chiều cao của các bạn chủ yếu thuộc vào khoảng 140 cm đến 141 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.