Cho hình chóp S.ABCD, đáy ABCD là hình bình hành, mặt phẳng đi qua AB cắt cạnh SC, SD lần lượt tại M, N. Tính tỉ số để chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau.
A.
B.
C.
D.
Quảng cáo
Trả lời:
Chọn C
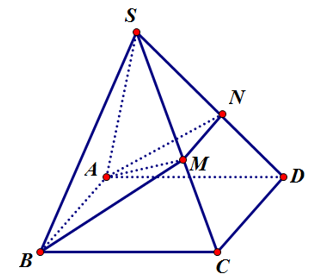
Ta có: .
Do đó là (ABMN).
Mặt phẳng chia khối chóp thành 2 phần có thể tích bằng nhau là
Ta có:
Đặt với (0<x<1), khi đó theo Ta-let ta có .
Mặt khác
Từ (1), (2) suy ra
Đối chiếu điều kiện của x ta được
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án là B

Cách 1. Xác định và tính góc giữa hai đường thẳng.
Tam giác ABC vuông tại A
![]()
Do SA=SB=SC nên nếu gọi H là hình chiếu vuông góc của S lên (ABC) thì H là tâm đường tròn ngoại tiếp tam giác ABC mà tam giác ABC vuông tại A nên H là trung điểm của BC.
Dựng hình bình hành ABCD. Khi đó:(AB,SC)=(CD,SC) và CD=AB=a. Tam giác SBC vuông tại S
![]()
có SH là đường trùng tuyến nên SH=
Tam giác CDH có
![]()
theo định lý Cô- Sin ta có
![]()
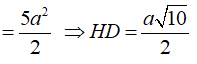
Tam giác SHD vuông tại H nên
![]()
Tam giác SCD có:
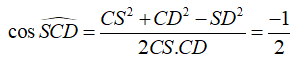
![]()
![]()
Cách 2. (Hay phù hợp với bài này) Ứng dụng tích vô hướng.
![]()
Theo giả thiết có
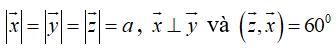
Ta có
![]()
![]()
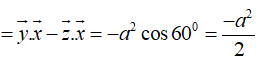
Suy ra:
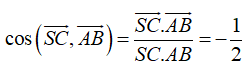
![]()
![]()
Lời giải
Đáp án là B
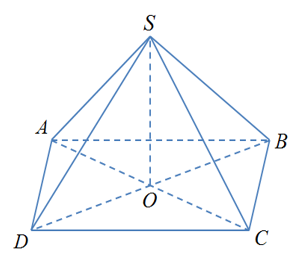
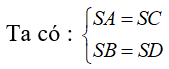
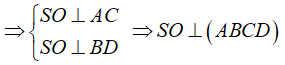
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
