Câu hỏi:
11/07/2024 1,250
Trong trò chơi "Vòng quay may mắn", người chơi sẽ quay hai bánh xe. Mũi tên ở bánh xe thứ nhất có thể dừng ở một trong hai vị trí: Loại xe 50 cc và Loại xe 110 cc. Mũi tên ở bánh xe thứ hai có thể dừng ở một trong bốn vị trí: màu đen, màu trắng, màu đỏ và màu xanh. Vị trí của mũi tên trên hai bánh xe sẽ xác định người chơi nhận được loại xe nào, màu gì.
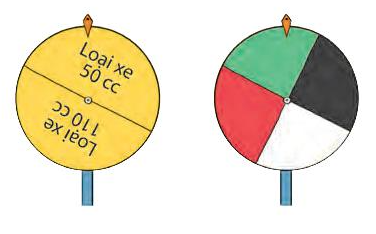
Phép thử T là quay hai bánh xe. Hãy vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
Trong trò chơi "Vòng quay may mắn", người chơi sẽ quay hai bánh xe. Mũi tên ở bánh xe thứ nhất có thể dừng ở một trong hai vị trí: Loại xe 50 cc và Loại xe 110 cc. Mũi tên ở bánh xe thứ hai có thể dừng ở một trong bốn vị trí: màu đen, màu trắng, màu đỏ và màu xanh. Vị trí của mũi tên trên hai bánh xe sẽ xác định người chơi nhận được loại xe nào, màu gì.
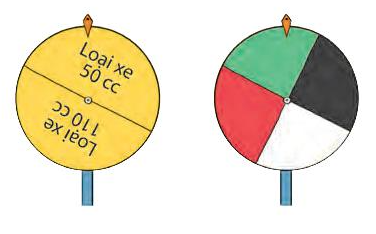
Phép thử T là quay hai bánh xe. Hãy vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
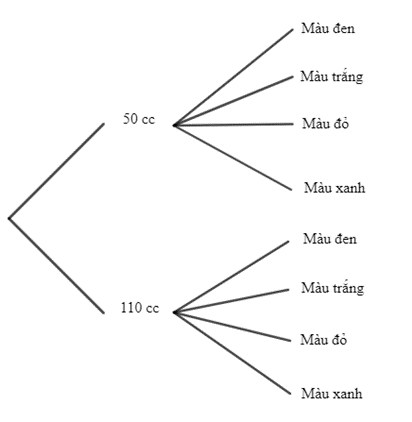
Theo bài ra, ta vẽ được sơ đồ hình cây mô tả các phần tử của không gian mẫu của phép thử T như sau:
Hot: Đề thi cuối kì 2 Toán, Văn, Anh.... file word có đáp án chi tiết lớp 1-12 form 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025
Đã bán 100
₫ 40.500
₫ 13.600
Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025
Đã bán 321
₫ 136.000
₫ 40.000
Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack
Đã bán 218
₫ 130.000
₫ 75.000
Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack
Đã bán 1k
₫ 104.000
₫ 52.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
B. Bài tập
Chọn ngẫu nhiên một gia đình có ba con và quan sát giới tính của ba người con này. Tính xác suất của các biến cố sau:
a) A: “Con đầu là gái”;
b) B: “Có ít nhất một người con trai”.
B. Bài tập
Chọn ngẫu nhiên một gia đình có ba con và quan sát giới tính của ba người con này. Tính xác suất của các biến cố sau:
a) A: “Con đầu là gái”;
b) B: “Có ít nhất một người con trai”.
Xem đáp án »
11/07/2024
29,856
Câu 2:
Một chiếc hộp đựng 6 viên bi trắng, 4 viên bi đỏ và 2 viên bi đen. Chọn ngẫu nhiên ra 6 viên bi. Tính xác suất để trong 6 viên bi đó có 3 viên bi trắng, 2 viên bi đỏ và 1 viên bi đen.
Một chiếc hộp đựng 6 viên bi trắng, 4 viên bi đỏ và 2 viên bi đen. Chọn ngẫu nhiên ra 6 viên bi. Tính xác suất để trong 6 viên bi đó có 3 viên bi trắng, 2 viên bi đỏ và 1 viên bi đen.
Xem đáp án »
11/07/2024
18,867
Câu 3:
Gieo lần lượt hai con xúc xắc cân đối. Tính xác suất để ít nhất một con xúc xắc xuất hiện mặt 6 chấm.
Xem đáp án »
11/07/2024
18,472
Câu 4:
Gieo liên tiếp một con xúc xắc cân đối và một đồng xu cân đối.
a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
b) Tính xác suất của các biến cố sau:
F: “Đồng xu xuất hiện mặt ngửa”;
G: “Đồng xu xuất hiện mặt sấp hoặc số chấm xuất hiện trên con xúc xắc là 5”.
Gieo liên tiếp một con xúc xắc cân đối và một đồng xu cân đối.
a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
b) Tính xác suất của các biến cố sau:
F: “Đồng xu xuất hiện mặt ngửa”;
G: “Đồng xu xuất hiện mặt sấp hoặc số chấm xuất hiện trên con xúc xắc là 5”.
Xem đáp án »
11/07/2024
14,074
Câu 5:
Một hộp đựng các tấm thẻ đánh số 10; 11; ....; 20. Rút ngẫu nhiên từ hộp hai tấm thẻ. Tính xác suất của các biến cố sau:
a) C: “Cả hai thẻ rút được đều mang số lẻ”;
b) D: “Cả hai thẻ rút được đều mang số chẵn”.
Một hộp đựng các tấm thẻ đánh số 10; 11; ....; 20. Rút ngẫu nhiên từ hộp hai tấm thẻ. Tính xác suất của các biến cố sau:
a) C: “Cả hai thẻ rút được đều mang số lẻ”;
b) D: “Cả hai thẻ rút được đều mang số chẵn”.
Xem đáp án »
11/07/2024
13,748
Câu 6:
Một tổ trong lớp 10B có 12 học sinh, trong đó có 7 học sinh nam và 5 học sinh nữ. Giáo viên chọn ngẫu nhiên 6 học sinh trong tổ để kiểm tra vở bài tập Toán. Tính xác suất để trong 6 học sinh được chọn số học sinh nữ bằng số học sinh nam.
Một tổ trong lớp 10B có 12 học sinh, trong đó có 7 học sinh nam và 5 học sinh nữ. Giáo viên chọn ngẫu nhiên 6 học sinh trong tổ để kiểm tra vở bài tập Toán. Tính xác suất để trong 6 học sinh được chọn số học sinh nữ bằng số học sinh nam.
Xem đáp án »
11/07/2024
11,163
Câu 7:
Màu hạt của đậu Hà Lan có hai kiểu hình là màu vàng và màu xanh tương ứng với hai loại gene là gene trội A và gene lặn a. Hình dạng hạt của đậu Hà Lan có hai kiểu hình là hạt trơn và hạt nhăn tương ứng với hai loại gene là gene trội B và gene lặn b. Biết rằng, cây con lấy ngẫu nhiên một gene từ cây bố và một gene từ cây mẹ.
Phép thử là cho lai hai loại đậu Hà Lan, trong đó cả cây bố và cây mẹ đều có kiểu gene là (Aa, Bb) và kiểu hình là hạt màu vàng và trơn. Giả sử các kết quả có thể là đồng khả năng. Tính xác suất để cây con cũng có kiểu hình là hạt màu vàng và trơn.
Màu hạt của đậu Hà Lan có hai kiểu hình là màu vàng và màu xanh tương ứng với hai loại gene là gene trội A và gene lặn a. Hình dạng hạt của đậu Hà Lan có hai kiểu hình là hạt trơn và hạt nhăn tương ứng với hai loại gene là gene trội B và gene lặn b. Biết rằng, cây con lấy ngẫu nhiên một gene từ cây bố và một gene từ cây mẹ.
Phép thử là cho lai hai loại đậu Hà Lan, trong đó cả cây bố và cây mẹ đều có kiểu gene là (Aa, Bb) và kiểu hình là hạt màu vàng và trơn. Giả sử các kết quả có thể là đồng khả năng. Tính xác suất để cây con cũng có kiểu hình là hạt màu vàng và trơn.
Xem đáp án »
11/07/2024
11,035
🔥 Đề thi HOT:
-
10 Bài tập Ứng dụng ba đường conic vào các bài toán thực tế (có lời giải)
-
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
-
12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)
-
185 câu Trắc nghiệm Toán 10 Bài 1:Phương trình đường thẳng trong mặt phẳng oxy có đáp án (Mới nhất)
-
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
-
10 Bài tập Các bài toán thực tế ứng dụng nhị thức Newton (có lời giải)
-
Bộ 5 đề thi cuối kì 2 Toán 10 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
-
10 Bài tập Viết phương trình cạnh, đường cao, trung tuyến, phân giác của tam giác (có lời giải)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận