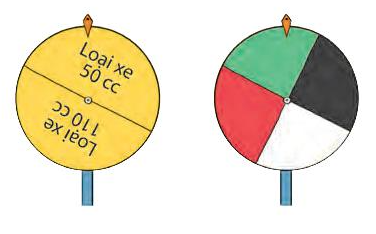Bài tập Bài 27. Thực hành tính xác suất theo định nghĩa cổ điển có đáp án
38 người thi tuần này 4.6 1.3 K lượt thi 16 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 3
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 2
Đề kiểm tra Ôn tập chương 9 (có lời giải) -Đề 1
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải
Phép thử của bài toán là chọn ngẫu nhiên 6 số trong 45 số: 1; 2; 3; …; 45. Không gian mẫu Ω là tập hợp tất cả các tập con có 6 phần tử của tập {1; 2; 3; …; 45}.
Do đó số phần tử của không gian mẫu là n(Ω) = \(C_{45}^6\).
+ Gọi F là biến cố: “Bạn An trúng giải độc đắc”.
Ta có: F là tập hợp có duy nhất 1 phần tử là tập {5; 13; 20; 31; 32; 35}. Do đó, n(F) = 1.
Vậy xác suất để bạn An trúng giải độc đắc là \(P\left( F \right) = \frac{{n\left( F \right)}}{{n\left( \Omega \right)}} = \frac{1}{{C_{45}^6}} = \frac{1}{{8\,\,145\,\,060}}\).
+ Gọi G là biến cố: “Bạn An trúng giải nhất”.
Vì nếu bộ số của người chơi trùng với 5 số của bộ số trúng thưởng thì người chơi trúng giải nhất.
Do đó G là tập hợp tất cả các tập con gồm 6 phần tử của tập {1; 2; 3; …; 45} có tính chất: năm phần tử của nó thuộc tập {5; 13; 20; 31; 32; 35} và một phần tử còn lại không thuộc tập {5; 13; 20; 31; 32; 35}. Nghĩa là phần tử còn lại này phải thuộc tập {1; 2; 3; …; 45} \ {5; 13; 20; 31; 32; 35} (tập hợp này gồm 45 – 6 = 39 phần tử).
Mỗi phần tử của G được hình thành từ hai công đoạn.
Công đoạn 1. Chọn 5 phần tử trong tập {5; 13; 20; 31; 32; 35}, có \(C_6^5\) cách chọn.
Công đoạn 2. Chọn 1 phần tử trong 39 phần tử còn lại, có \(C_{39}^1\) cách chọn.
Theo quy tắc nhân, số phần tử của G là: n(G) = \(C_6^5.C_{39}^1 = 234\) (phần tử).
Vậy xác suất để bạn An trúng giải nhất là \(P\left( G \right) = \frac{{n\left( G \right)}}{{n\left( \Omega \right)}} = \frac{{234}}{{C_{45}^6}} = \frac{{39}}{{1\,\,357\,510}}\).
Lời giải
Hướng dẫn giải
Ta không thể tính n(Ω), n(F), n(G) bằng cách liệt kê hết được các phần tử của Ω, F, G rồi kiểm đếm, vì số các tập con gồm 6 phần tử của tập {1; 2; ...; 45} là quá lớn.
Lời giải
Hướng dẫn giải
Không gian mẫu là tập tất cả các tập con gồm 6 học sinh trong 12 học sinh.
Do đó, n(Ω) = \(C_{12}^6\) = 924.
Gọi biến cố A: “6 học sinh được chọn số học sinh nữ bằng số học sinh nam”.
Để số học sinh nữ bằng số học sinh nam thì chọn 3 nữ và 3 nam.
Mỗi phần tử của A được hình thành từ hai công đoạn.
Công đoạn 1. Chọn 3 học sinh nữ từ 5 học sinh nữ, có \(C_5^3 = 10\) (cách chọn).
Công đoạn 2. Chọn 3 học sinh nam từ 7 học sinh nam, có \(C_7^3 = 35\) (cách chọn).
Theo quy tắc nhân, tập A có 10 . 35 = 350 (phần tử). Do đó, n(A) = 350.
Vậy \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{350}}{{924}} = \frac{{25}}{{66}}\).
Lời giải
Hướng dẫn giải
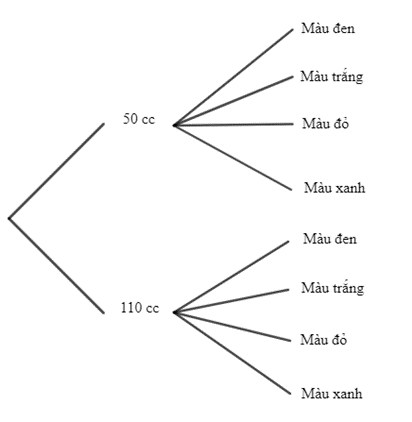
Theo bài ra, ta vẽ được sơ đồ hình cây mô tả các phần tử của không gian mẫu của phép thử T như sau:
Lời giải
Hướng dẫn giải
Theo như sơ đồ cây ở HĐ2, ta có n(Ω) = 8.
Gọi biến cố A: “Người chơi nhận được loại xe 110 cc có màu trắng hoặc màu xanh”.
Ta có n(A) = 2.
Vậy \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{2}{8} = \frac{1}{4}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.