Giải SBT Toán 10 Bài 11. Tích vô hướng của hai vectơ có đáp án

Lời giải

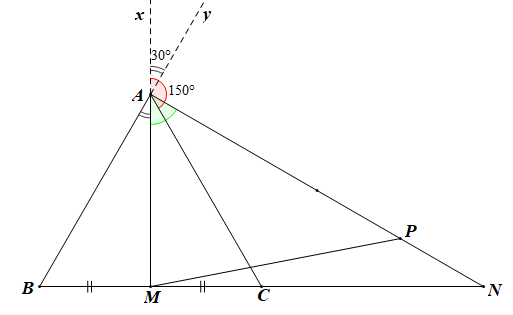
Tam giác ABC đều có M là trung điểm của BC nên đường trung tuyến AM đồng thời là đường phân giác và đường cao.

\( \Rightarrow \widehat {BAM} = \widehat {MAC} = \frac{1}{2}\widehat {BAC} = \frac{1}{2}.60^\circ = 30^\circ \)

Gọi Ax là tia đối của tia AM, tia Ay là tia đối của tia AB.

Do đó \(\left( {\overrightarrow {MA} ;\overrightarrow {BA} } \right) = \widehat {xAy} = \widehat {BAM} = 30^\circ \)

\(\left( {\overrightarrow {MA} ;\overrightarrow {AC} } \right) = \widehat {xAC} = 180^\circ - \widehat {MAC}\)

\( \Rightarrow \left( {\overrightarrow {MA} ;\overrightarrow {AC} } \right) = 180^\circ - 30^\circ = 150^\circ \)

Khi đó ta có:

• \(\overrightarrow {MA} .\overrightarrow {BA} = \left| {\overrightarrow {MA} } \right|.\left| {\overrightarrow {BA} } \right|.c{\rm{os}}\left( {\overrightarrow {MA} ;\overrightarrow {BA} } \right)\)

\( \Rightarrow \overrightarrow {MA} .\overrightarrow {BA} = MA.BA.c{\rm{os30}}^\circ \)

Xét tam giác BAM vuông tại M, theo định lí Pythagoras ta có:

\(MA = \sqrt {B{A^2} - B{M^2}} = \sqrt {{1^2} - {{\left( {\frac{1}{2}} \right)}^2}} = \frac{{\sqrt 3 }}{2}\)

\( \Rightarrow \overrightarrow {MA} .\overrightarrow {BA} = \frac{{\sqrt 3 }}{2}.1.\frac{{\sqrt 3 }}{2} = \frac{3}{4}.\)

• \(\overrightarrow {MA} .\overrightarrow {AC} = \left| {\overrightarrow {MA} } \right|.\left| {\overrightarrow {AC} } \right|.c{\rm{os}}\left( {\overrightarrow {MA} ;\overrightarrow {AC} } \right)\)

\( \Rightarrow \overrightarrow {MA} .\overrightarrow {AC} = MA.AC.c{\rm{os150}}^\circ \)

\[ \Rightarrow \overrightarrow {MA} .\overrightarrow {AC} = \frac{{\sqrt 3 }}{2}.1.\frac{{ - \sqrt 3 }}{2} = \frac{{ - 3}}{4}.\]

Vậy \(\overrightarrow {MA} .\overrightarrow {BA} = \frac{3}{4}\) và \(\overrightarrow {MA} .\overrightarrow {AC} = \frac{{ - 3}}{4}.\)

Lời giải

• Vì M là trung điểm của BC nên

\(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \)

\( \Rightarrow \overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)

• N đối xứng với B qua C nên C là trung điểm của BN

\( \Rightarrow \overrightarrow {AB} + \overrightarrow {AN} = 2\overrightarrow {AC} \)\( \Rightarrow \overrightarrow {AN} = 2\overrightarrow {AC} - \overrightarrow {AB} \)

Khi đó \(\overrightarrow {AM} .\overrightarrow {AN} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\left( {2\overrightarrow {AC} - \overrightarrow {AB} } \right)\)

\[ = \frac{1}{2}.\left( {2\overrightarrow {AB} .\overrightarrow {AC} - \overrightarrow {AB} .\overrightarrow {AB} + 2\overrightarrow {AC} .\overrightarrow {AC} - \overrightarrow {AC} .\overrightarrow {AB} } \right)\]

\[ = \frac{1}{2}.\left( {2{{\overrightarrow {AC} }^2} - {{\overrightarrow {AB} }^2} + \overrightarrow {AB} .\overrightarrow {AC} } \right)\]

\[ = \frac{1}{2}.\left( {2{{\left| {\overrightarrow {AC} } \right|}^2} - {{\left| {\overrightarrow {AB} } \right|}^2} + \overrightarrow {AB} .\overrightarrow {AC} } \right)\]

Mà \[\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.cos\left( {\overrightarrow {AB} .\overrightarrow {AC} } \right)\]

\[ = AB.AC.cos\widehat {BAC} = 1.1.\cos 60^\circ = \frac{1}{2}.\]

Do đó \(\overrightarrow {AM} .\overrightarrow {AN} \)\[ = \frac{1}{2}.\left( {2A{C^2} - A{B^2} + \overrightarrow {AB} .\overrightarrow {AC} } \right)\]

\[ = \frac{1}{2}.\left( {{{2.1}^2} - {1^2} + \frac{1}{2}} \right)\]

\( = \frac{1}{2}.\frac{3}{2} = \frac{3}{4}.\)

Vậy \(\overrightarrow {AM} .\overrightarrow {AN} = \frac{3}{4}\)

Lời giải

• Vì P thuộc đoạn thẳng AN thỏa mãn AP = 3PN \( \Rightarrow AP = \frac{3}{4}AN\)

\( \Rightarrow \overrightarrow {AP} = \frac{3}{4}\overrightarrow {AN} = \frac{3}{4}.\left( {2\overrightarrow {AC} - \overrightarrow {AB} } \right)\)

\( \Rightarrow \overrightarrow {AP} = \frac{3}{2}\overrightarrow {AC} - \frac{3}{4}\overrightarrow {AB} \)

• Ta có: \(\overrightarrow {MP} = \overrightarrow {AP} - \overrightarrow {AM} \)

\( = \left( {\frac{3}{2}\overrightarrow {AC} - \frac{3}{4}\overrightarrow {AB} } \right) - \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)

\( = \frac{3}{2}\overrightarrow {AC} - \frac{3}{4}\overrightarrow {AB} - \frac{1}{2}\overrightarrow {AB} - \frac{1}{2}\overrightarrow {AC} \)

\( = \left( {\frac{3}{2}\overrightarrow {AC} - \frac{1}{2}\overrightarrow {AC} } \right) - \left( {\frac{3}{4}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AB} } \right)\)

\( = \overrightarrow {AC} - \frac{5}{4}\overrightarrow {AB} \)

\( \Rightarrow MP = \left| {\overrightarrow {MP} } \right| = \left| {\overrightarrow {AC} - \frac{5}{4}\overrightarrow {AB} } \right|\)

\( \Rightarrow M{P^2} = {\left( {\overrightarrow {AC} - \frac{5}{4}\overrightarrow {AB} } \right)^2}\)

\( = {\overrightarrow {AC} ^2} - 2.\frac{5}{4}\overrightarrow {AC} .\overrightarrow {AB} + \frac{{25}}{{16}}{\overrightarrow {AB} ^2}\)

\( = A{C^2} + \frac{{25}}{{16}}A{B^2} - \frac{5}{2}\overrightarrow {AC} .\overrightarrow {AB} \)

\( = {1^2} + \frac{{25}}{{16}}{.1^2} - \frac{5}{2}.\frac{1}{2}\)

\( = \frac{{21}}{{16}}\)

\( \Rightarrow MP = \sqrt {\frac{{21}}{{16}}} = \frac{{\sqrt {21} }}{4}.\)

Vậy \(\overrightarrow {AP} = \frac{3}{2}\overrightarrow {AC} - \frac{3}{4}\overrightarrow {AB} ;\)\(\overrightarrow {MP} = \overrightarrow {AC} - \frac{5}{4}\overrightarrow {AB} \) và \(MP = \frac{{\sqrt {21} }}{4}.\)

Lời giải

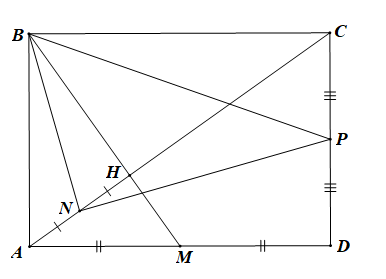
a) Đặt \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AD} = \overrightarrow b \) khi đó \(\left| {\overrightarrow a } \right| = 1\)và \(\left| {\overrightarrow b } \right| = \sqrt 2 .\)

Vì AB ⊥ AD nên \(\overrightarrow a \bot \overrightarrow b \Leftrightarrow \overrightarrow a .\overrightarrow b = \overrightarrow 0 \)

ABCD là hình chữ nhật nên cũng là hình bình hành nên ta có:

\(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow a + \overrightarrow b \) (quy tắc hình bình hành)

M là trung điểm của AD nên \(\overrightarrow {AM} = \frac{1}{2}\overrightarrow {AD} = \frac{1}{2}\overrightarrow b \)

Suy ra \(\overrightarrow {BM} = \overrightarrow {AM} - \overrightarrow {AB} = \frac{1}{2}\overrightarrow b - \overrightarrow a \)

Khi đó \(\overrightarrow {AC} .\overrightarrow {BM} = \left( {\overrightarrow a + \overrightarrow b } \right).\left( {\frac{1}{2}\overrightarrow b - \overrightarrow a } \right)\)

\( = \frac{1}{2}\overrightarrow a .\overrightarrow b - \overrightarrow a .\overrightarrow a + \frac{1}{2}\overrightarrow b .\overrightarrow b - \overrightarrow a .\overrightarrow b \)

\( = \frac{1}{2}\overrightarrow 0 - {\overrightarrow a ^2} + \frac{1}{2}{\overrightarrow b ^2} - \overrightarrow 0 \) (do \(\overrightarrow a .\overrightarrow b = \overrightarrow 0 \))

\( = - {\left| {\overrightarrow a } \right|^2} + \frac{1}{2}{\left| {\overrightarrow b } \right|^2}\)

\( = - {1^2} + \frac{1}{2}.{\left( {\sqrt 2 } \right)^2} = 0\)

Do đó \(\overrightarrow {AC} .\overrightarrow {BM} = 0 \Leftrightarrow \overrightarrow {AC} \bot \overrightarrow {BM} \)

AC ⊥ BM.

Lời giải

• Xét tam giác ABC vuông tại C, theo định lí Pythagore ta có:

AC² = AB² + BC² = 1 + \({\left( {\sqrt 2 } \right)^2}\)= 3

\( \Rightarrow AC = \sqrt 3 \)

Theo hệ thức lượng trong tam giác vuông ta có:

AB² = AH.AC \( \Rightarrow AH = \frac{{A{B^2}}}{{AC}} = \frac{{{1^2}}}{{\sqrt 3 }} = \frac{{\sqrt 3 }}{3}\)

\[ \Rightarrow \frac{{AH}}{{AC}} = \frac{{\sqrt 3 }}{3}:\sqrt 3 = \frac{1}{3}\]

\( \Rightarrow \overrightarrow {AH} = \frac{1}{3}\overrightarrow {AC} \)

Khi đó \(\overrightarrow {HC} = \frac{2}{3}\overrightarrow {AC} \) và \(\overrightarrow {HA} = - \frac{1}{3}\overrightarrow {AC} \)

Ta có \(\overrightarrow {NB} = \overrightarrow {NA} + \overrightarrow {AB} \) (quy tắc ba điiểm)

Vì N là trung điểm của AH nên \(\overrightarrow {NA} = \frac{1}{2}\overrightarrow {HA} \)

\( \Rightarrow \overrightarrow {NB} = \frac{1}{2}.\left( { - \frac{1}{3}\overrightarrow {AC} } \right) + \overrightarrow {AB} \)

\( = - \frac{1}{6}.\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow a \)

\( = \frac{5}{6}\overrightarrow a - \frac{1}{6}\overrightarrow b \)

• Có N là trung điểm của HA và P là trung điểm của CD, theo kết quả bài 4.12, trang 58, Sách giáo khoa Toán 10, tập một, ta có:

\(\overrightarrow {AD} + \overrightarrow {HC} = 2\overrightarrow {NP} \)\( \Rightarrow \overrightarrow {NP} = \frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {HC} } \right)\)

\( \Rightarrow \overrightarrow {NP} = \frac{1}{2}\overrightarrow {AD} + \frac{1}{2}\overrightarrow {HC} \)

\( = \frac{1}{2}\overrightarrow {AD} + \frac{1}{2}.\frac{2}{3}\overrightarrow {AC} \)

\( = \frac{1}{2}\overrightarrow b + \frac{1}{3}.\left( {\overrightarrow a + \overrightarrow b } \right)\)

\( = \frac{1}{3}\overrightarrow a + \frac{5}{6}.\overrightarrow b \)

Khi đó \[\overrightarrow {NB} .\overrightarrow {NP} = \left( {\frac{5}{6}\overrightarrow a - \frac{1}{6}\overrightarrow b } \right).\left( {\frac{1}{3}\overrightarrow a + \frac{5}{6}.\overrightarrow b } \right)\]

\[ = \frac{5}{{18}}{\overrightarrow a ^2} + \frac{{25}}{{36}}\overrightarrow a .\overrightarrow b - \frac{1}{{18}}\overrightarrow a .\overrightarrow b - \frac{5}{{36}}{\overrightarrow b ^2}\]

\[ = \frac{5}{{18}}{\overrightarrow a ^2} + \frac{{25}}{{36}}\overrightarrow a .\overrightarrow b - \frac{1}{{18}}\overrightarrow a .\overrightarrow b - \frac{5}{{36}}{\overrightarrow b ^2}\]

\[ = \frac{5}{{18}}{\left| {\overrightarrow a } \right|^2} + \frac{{25}}{{36}}\overrightarrow 0 - \frac{1}{{18}}\overrightarrow 0 - \frac{5}{{36}}{\left| {\overrightarrow b } \right|^2}\] (do \(\overrightarrow a .\overrightarrow b = \overrightarrow 0 \))

\[ = \frac{5}{{18}}{.1^2} - \frac{5}{{36}}.{\left( {\sqrt 2 } \right)^2}\]

\[ = \frac{5}{{18}} - \frac{5}{{36}}.2 = 0\]

Do đó \[\overrightarrow {NB} .\overrightarrow {NP} = 0 \Rightarrow \overrightarrow {NB} \bot \overrightarrow {NP} \]

NB ⊥ NP.