Bài tập Bài 16. Hàm số bậc hai có đáp án
89 người thi tuần này 4.6 2 K lượt thi 17 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
20 câu trắc nghiệm Toán 10 Cánh diều Bài tập cuối chương 7 (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 6. Ba đường conic (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 5. Phương trình đường trò (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 4. Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 3. Phương trình đường thẳn (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 2. Biểu thức tọa độ của các phép toán vectơ (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 1. Tọa độ của vectơ (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài ôn tập cuối chương 6 (Đúng sai - trả lời ngắn) có đáp án
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải
Sau bài học này, ta giải quyết được bài toán trên như sau:
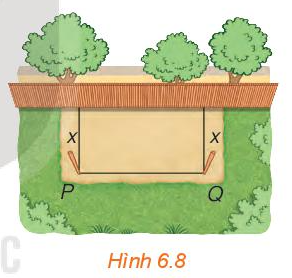
Gọi x (mét, x > 0) là khoảng cách từ điểm cọc P và Q đến bờ tường.
Tấm lưới dài 20 m và được rào chắn ba mặt áp lên bờ tường như Hình 6.8, do đó ta có:
x + x + PQ = 20.
Suy ra: PQ = 20 – x – x = 20 – 2x (m).
Vì PQ > 0 (độ dài dương) nên 20 – 2x > 0 ⇔ 2x < 20 ⇔ x < 10.
Do đó ta có điều kiện của x là 0 < x < 10.
Mảnh đất được rào chắn có dạng hình chữ nhật với hai kích thước là x (m) và 20 – 2x (m) với 0 < x < 10.
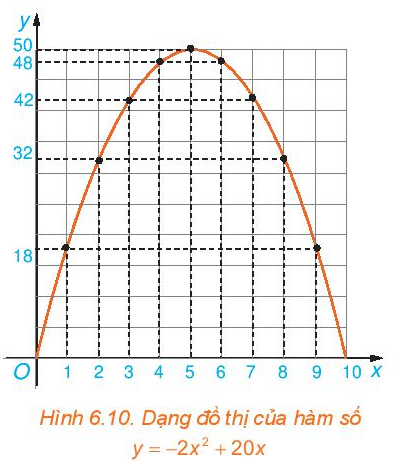
Khi đó diện tích của mảnh đất là S(x) = x . (20 – 2x) = – 2x2 + 20x.
Theo yêu cầu bài toán, ta cần tìm giá trị của x để S(x) có giá trị lớn nhất.
Ta có: S(x) = – 2(x2 – 10x) = – 2(x2 – 2 . 5 . x + 25) + 50 = – 2(x – 5)2 + 50 ≤ 50 với mọi số thực x.
Dấu “=” xảy ra khi x – 5 = 0 ⇔ x = 5 (thỏa mãn điều kiện 0 < x < 10).
Do đó giá trị lớn nhất của S(x) là 50 tại x = 5.
Vậy hai cột góc hàng rào cần phải cắm cách bờ tường 5 m để mảnh đất được rào chắn của bác Việt có diện tích lớn nhất.
Lời giải
Hướng dẫn giải
a) Tấm lưới có chiều dài 20 m, khoảng cách từ điểm cắm cọc tới bờ tường là x (m), ta đóng 2 cọc P và Q, mỗi cọc đều cách tường x (m).
Tấm lưới rào chắn 3 mặt áp bên bờ tường như Hình 6.8 nên x + x + PQ = 20.
Do đó độ dài cạnh PQ của mảnh đất là:
20 – x – x = 20 – 2x (m).
b) Mảnh đất được rào chắn là một hình chữ nhật có hai kích thước là x (m) và 20 – 2x (m).
Do đó diện tích S(x) của mảnh đất được rào chắn là:
S(x) = x . (20 – 2x) = – 2x2 + 20x.
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
Hàm số bậc hai là hàm số cho bởi công thức y = ax2 + bx + x với a, b, c là các hằng số và a ≠ 0.
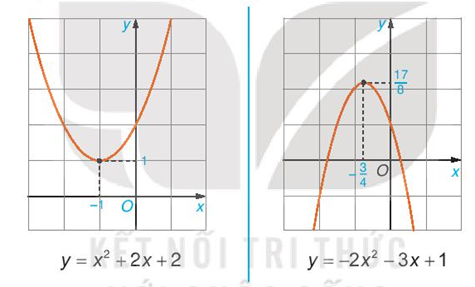
Vậy trong các hàm số đã cho thì hàm số y = – 3x2 + 1 là hàm số bậc hai với các hệ số a = – 3, b = 0 và c = 1.
Chú ý: Hàm số \(y = 3{\left( {\frac{1}{x}} \right)^2} + 3\frac{1}{x} - 1\) không phải là hàm số bậc hai, mà đây là hàm số có thể đưa về dạng bậc hai nếu ta đặt \(t = \frac{1}{x}\).
Lời giải
Hướng dẫn giải
a) Ta có: y = (x – 1)(2 – 3x) = 2x – 3x2 – 2 + 3x = – 3x2 + 5x – 2.
Suy ra y = – 3x2 + 5x – 2, đây là hàm số bậc hai với các hệ số a = – 3, b = 5, c = – 2.
b) Với x = – 2 thì y = – 3 . (– 2)2 + 5 . (– 2) – 2 = – 24.
Với x = – 1 thì y = – 3 . (– 1)2 + 5 . (– 1) – 2 = – 10.
Với x = 0 thì y = – 3 . 02 + 5 . 0 – 2 = – 2.
Với x = 1 thì y = – 3 . 12 + 5 . 1 – 2 = 0.
Vậy ta có bảng sau:
|
x |
– 2 |
– 1 |
0 |
1 |
|
y |
– 24 |
– 10 |
– 2 |
0 |
Lời giải
Hướng dẫn giải
a) Viên bi rơi chạm đất thì h = 0.
Khi đó: 19,6 – 4,9t2 = 0 ⇔ 4,9t2 = 19,6 ⇔ t2 = 4 ⇔ t = 2 hoặc t = – 2.
Vì t ≥ 0 nên ta chọn t = 2.
Vậy sau 2 giây kể từ khi rơi thì viên bi chạm đất.
b) Ta có: h = 19,6 – 4,9t2
Đây là hàm số bậc hai với biến t, mà t ≥ 0.
Do đó, tập xác định của hàm số h này là D = [0; + ∞).
Vì t2 ≥ 0 với mọi t nên – 4,9t2 ≤ 0 với mọi t.
Suy ra – 4,9t2 + 19,6 ≤ 0 + 19,6 hay 19,6 – 4,9t2 ≤ 19,6 với mọi t.
Do đó: h ≤ 19,6 với mọi t.
Mặt khác, h ≥ 0.
Khi đó: 0 ≤ h ≤ 19,6 với mọi t.
Vậy tập giá trị của hàm số h là [0; 19,6].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.